Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Howie, J. M.
1981.
Some subsemigroups of infinite full transformation semigroups.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 88,
Issue. 1-2,
p.
159.
Howie, J. M.
1981.
A congruence-free inverse semigroup associated with a pair of infinite cardinals.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 31,
Issue. 3,
p.
337.
Marques, M. Paula O.
1983.
A congruence-free semigroup associated with an infinite cardinal number.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 93,
Issue. 3-4,
p.
245.
Howie, John M.
and
Marques-Smith, M. Paula O.
1984.
Inverse semigroups generated by nilpotent transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 99,
Issue. 1-2,
p.
153.
Munn, W. D.
1985.
Congruence-free regular semigroups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 28,
Issue. 1,
p.
113.
Howie, John M.
and
Marques-Smith, M. Paula O.
1988.
A nilpotent-generated semigroup associated with a semigroup of full transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 108,
Issue. 1-2,
p.
181.
Byleen, Karl
1990.
Embedding any countable semigroup in a 2-generated congruence-free semigroup.
Semigroup Forum,
Vol. 41,
Issue. 1,
p.
145.
Marques-Smith, M. Paula O.
and
Sullivan, R.P.
1999.
The ideal structure of nilpotent-generated transformation semigroups.
Bulletin of the Australian Mathematical Society,
Vol. 60,
Issue. 2,
p.
303.
Marques-Smith, M.Paula O.
and
Sullivan, R.P.
2000.
The Congruences on the Semigroup of Balanced Transformations of an Infinite Set.
Journal of Algebra,
Vol. 234,
Issue. 1,
p.
1.
Sanwong, Jintana
and
Sullivan, R. P.
2007.
Maximal Congruences on Some Semigroups.
Algebra Colloquium,
Vol. 14,
Issue. 02,
p.
255.
Yu, Houyi
Wang, Zhengpan
Wu, Tongsuo
and
Ye, Meng
2012.
Classification of some τ-congruence-free completely regular semigroups.
Semigroup Forum,
Vol. 84,
Issue. 2,
p.
308.
Gomes, Gracinda M. S.
and
Ruškuc, Nik
2014.
John Macintosh Howie: work and legacy.
Semigroup Forum,
Vol. 89,
Issue. 1,
p.
2.


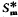 has both these properties and is also congruence-free. The semigroup
has both these properties and is also congruence-free. The semigroup 