Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T17:37:14.629Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds for the eigenvalues of separated Dirac operators

Published online by Cambridge University Press:  14 November 2011

B. J. Harris
B. J. Harris
Affiliation:
Department of Mathematical Sciences, Northern Illinois University, Dekalb, Illinois 60115, U.S.A
Get access Rights & Permissions [Opens in a new window]

Synopsis

We develop a systematic method for calculating real numbers Λ1, and Λ2 such that there are no non-trivial solutions of the equation

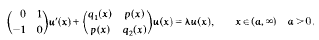
which belong to L2(a, ∞) for λ> Λ1, or λ < Λ2. We also give conditions under which this equation has no solutions in L2(a,∞) for any real number λ.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 95 , Issue 3-4 , 1983 , pp. 341 - 366
Copyright
Copyright © Royal Society of Edinburgh 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Atkinson, F. V. and Everitt, W. N.. Bounds for the point spectrum of a Sturm-Liouville equation. Proc. Roy. Soc. Edinburgh Sect. A 80 (1978), 57–66.CrossRefGoogle Scholar
2Eastham, M. S. P.. Sturm-Liouville equations and purely continuous spectra. Nieuw Arch. Wisk. 15 (1977), 169–181.Google Scholar
3Erdélyi, A.. Note on a paper of Titchmarsh. Quart. J. Math. Oxford 14 (1963), 147–152.Google Scholar
4Evans, W. D. and Harris, B. J.. Bounds for the point spectra of separated Dirac operators. Proc. Roy. Soc. Edinburgh Sect. A 88 (1980), 1–15.CrossRefGoogle Scholar
5Harris, B. J.. Bounds for the point spectra of Sturm-Liouville equations. J. London Math. Soc. 25 (1982), 145–161.CrossRefGoogle Scholar
6Harris, B. J.. Criteria for Sturm-Liouville equations to have continuous spectra. J. Math. Anal. Appl. 93, 1 (1983), 235–249.Google Scholar
7Titchmarsh, E. C.. On the nature of the spectrum in problems of relativistic quantum mechanics. Quart. J. Math. Oxford 12 (1961), 227–240.CrossRefGoogle Scholar
8Weidmann, J.. Oszillationmethoden für Systeme gewöhnlicher Differential gleichungen. Math. Z. 119 (1971), 349–373.CrossRefGoogle Scholar