Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T19:07:39.462Z Has data issue: false hasContentIssue false
  • English
  • Français

Blow-up time involved with perturbed Hamilton–Jacobi equations

Published online by Cambridge University Press:  14 November 2011

G. Díaz
G. Díaz
Affiliation:
Departamento de Matemática Aplicada, Universidad Complutense de Madrid, 28040-Madrid, Spain
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper we consider the evolution of positive bounded uniformly continuous data u0 by perturbed equations like

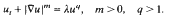
Under general assumptions on u0, existence, uniqueness and regularity of the evolution u in the set

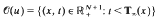
are studied, where the blow-up function is given by .

The exact blow-up rate of u is obtained. Uniqueness, regularity, decay at infinity of the function , as well a s a representation formula for the case m = 1, are also proved.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 122 , Issue 1-2 , 1992 , pp. 17 - 44
Copyright
Copyright © Royal Society of Edinburgh 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Barles, G.. First order Hamilton-Jacobi equations. Ann. Inst. H. Poincaré Anal. Non Linéarie (1984), 325–340.CrossRefGoogle Scholar
2Barles, G.. Remarks on a flame propagation model (Rapports de Recherche INRIA 464, 1985).Google Scholar
3Crandall, M. G., Evans, L. C. and Lions, P. L.. Some properties of viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 282 (1984), 487–502.CrossRefGoogle Scholar
4Crandall, M. G. and Lions, P. L.. Viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 277 (1983), 1–42.CrossRefGoogle Scholar
5Crandall, M. G. and Lions, P. L.. Remarks on the existence and uniqueness of unbounded viscosity solutions of Hamilton-Jacobi equations. Illinois J. Math. 31 (1987), 665–688.CrossRefGoogle Scholar
6Díaz, G.. The evolution by some perturbed Hamilton-Jacobi operators of an initial singularity (to appear).Google Scholar
7Díaz, G., (in preparation).Google Scholar
8Díaz, G. and Rey, J. M.. Finite extinction time for some perturbed Hamilton-Jacobi equations. Appl. Math. Optim. (to appear).Google Scholar
9D, G.íaz and Rey, J. M.. (in preparation).Google Scholar
10Elliot, R. J.. Viscosity solutions and optimal control (London: Pitman, 1987).Google Scholar
11Evans, L. C. and Souganidis, P. E.. A PDE approach to geometric optics for certain semilinear parabolic equations. Indiana Univ. Math. J. 38 (1989), 141–172.CrossRefGoogle Scholar
12Friedman, A. and Souganidis, P. E.. Blow-up of solutions of Hamilton-Jacobi equations. Comm. Partial Differential Equations 11(4) (1986), 397–443.CrossRefGoogle Scholar
13Ishii, H.. Uniqueness of unbounded viscosity solutions of Hamilton-Jacobi equations. Indiana Univ. Math. J. 33 (1984), 721–748.CrossRefGoogle Scholar
14Lions, P. L.. Generalized solutions of Hamilton-Jacobi equations (London: Pitman, 1982).Google Scholar
15Lions, P. L.. Existence results for first order Hamilton-Jacobi equations. Ricerche Mat. 32 (1983), 1–23.Google Scholar
16Lions, P. L., Souganidis, P. E. and Vazquez, J. L.. The relation between the porous medium and the eikonal equations in several space dimension. Revista Mat. Iberoamericana 3 (1987), 275–310.CrossRefGoogle Scholar
17Ross, D. S.. Ion etching: An application of the mathematical theory of hyperbolic conservation laws. J. Electrochemical Soc. 135(5) (1988), 1235–1240.CrossRefGoogle Scholar
18Serrin, J.. The problem of Dirichlet for quasilinear elliptic differential equations with many independent variables. Philos. Trans. Roy. Soc. London Ser. A 264 (1969), 413–496.Google Scholar
19Sethian, J.. An analysis of flame propagation (Ph.D. Dissertation, Lawrence Berkeley Laboratory, University of California, June 1982; CPAM Rep. 79).Google Scholar
20Souganidis, P. E.. Existence of viscosity solutions of Hamilton-Jacobi equations. J. Differential Equations 56 (1985), 345–390.CrossRefGoogle Scholar