Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T19:11:06.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation and standing wave solutions for a quasilinear Schrödinger equation

Part of: Spectral theory and eigenvalue problems Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  27 December 2018

Guowei Dai
Guowei Dai*
Affiliation:
School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, PR China ([email protected].)
Get access Rights & Permissions [Opens in a new window]

Abstract

We use bifurcation and topological methods to investigate the existence/nonexistence and the multiplicity of positive solutions of the following quasilinear Schrödinger equation

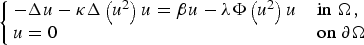$$\left\{ {\matrix{ {-\Delta u-\kappa \Delta \left( {u^2} \right)u = \beta u-\lambda \Phi \left( {u^2} \right)u{\mkern 1mu} {\mkern 1mu} } \hfill & {{\rm in}\;\Omega ,} \hfill \cr {u = 0} \hfill & {{\rm on}\;\partial \Omega } \hfill \cr } } \right.$$
involving sublinear/linear/superlinear nonlinearities at zero or infinity with/without signum condition. In particular, we study the changes in the structure of positive solution with κ as the varying parameter.

Keywords

Bifurcationpositive solutionsQuasilinear Schrödinger equation

MSC classification

Primary: 35B32: Bifurcation
Secondary: 35J60: Nonlinear elliptic equations 35P30: Nonlinear eigenvalue problems, nonlinear spectral theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 4 , August 2019 , pp. 939 - 968
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Amann, H.. Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Rew. 8 (1976), 620–709.Google Scholar
2Ambrosetti, A. and Hess, P.. Positive solutions of asymptotically linear elliptic eigenvalue problems. J. Math. Anal. Appl. 73 (1980), 411–422.Google Scholar
3Ambrosetti, A. and Malchiodi, A.. Nonlinear analysis and semilinear elliptic problems. Cambridge studies in Advanced Mathematics, vol. 104 (Cambridge: Cambridge Univ. Press, 2007).Google Scholar
4Ambrosetti, A., Brezis, H. and Cerami, G.. Combined effects of concave and positive nonlinearities in some elliptic problems. J. Funct. Anal. 122 (1994), 519–543.Google Scholar
5Ambrosetti, A., Azorero, J. G. and Peral, I.. Multiplicity results for some nonlinear elliptic equations. J. Funct. Anal. 137 (1996), 219–242.Google Scholar
6Arcoya, D. and Gámez, J. L.. Bifurcation theory and related problems: anti-maximum principle and resonance. Comm. Partial Differ. Equ. 26 (2001), 1879–1911.Google Scholar
7Bass, F. G. and Nasanov, N. N.. Nonlinear electromagnetic spin waves. Phys. Rep. 189 (1990), 165–223.Google Scholar
8Berestycki, H. and Lions, P. L.. Some applications of the method of super and subsolutions, in Bifurcation and nonlinear Eigenvalue problems. Lecture Notes in Mathematics,vol. 782,pp. 16–41 (Berlin: Springer-Verlag, 1980).Google Scholar
9Berestycki, H. and Lions, P. L.. Existence of solutions for nonlinear scalar field equatons: I. The ground state. Arch. Rational Mech. Anal. 82 (1983), 313–345.Google Scholar
10Borovskii, A. V. and Galkin, A. L.. Dynamical modulation of an ultrashort high-intensity laser pulse in matter. JETP 77 (1993), 562–573.Google Scholar
11Brandi, H. S. et al. Relativistic and ponderomotive self-focusing of a laser beam in a radially inhomogeneous plasma. Phys. Fluids B 5 (1993), 3539–3550.Google Scholar
12Chen, X. L. and Sudan, R. N.. Necessary and sufficient conditions for self-focusing of short ultraintense laser pulse. Phys. Rev. Lett. 70 (1993), 2082–2085.Google Scholar
13Coleman, S., Glazer, V. and Martin, A.. Action minima among solutions to a class of Eucidean scalar field equations. Comm. Math. Phys. 58 (1978), 211–221.Google Scholar
14Colin, M.. Stability of standing waves for a quasilinear Schrödinger equation in space dimension 2. Adv. Differ. Equ. 8 (2003), 1–28.Google Scholar
15Colin, M. and Jeanjean, L.. Solutions for a quasilinear Schrödinger equation: a dual approach. Nonlinear Anal. 56 (2004), 213–226.Google Scholar
16Dai, G.. Bifurcation and one-sign solutions of the p-Laplacian involving a nonlinearity with zeros. Discrete Contin. Dyn. Syst. 36 (2016a), 5323–5345.Google Scholar
17Dai, G.. Two Whyburn type topological theorems and its applications to Monge-Ampère equations. Calc. Var. Partial Differential Equations 55 (2016), no. 4, Art. 97, 28 pp.Google Scholar
18Dai, G.. Bifurcation and nonnegative solutions for problem with mean curvature operator on general domain. Indiana Univ. Math. J. 67 (2018), 2103–2121.Google Scholar
19Dai, G. and Ma, R.. Unilateral global bifurcation phenomena and nodal solutions for p-Laplacian. J. Differ. Equ. 252 (2012), 2448–2468.Google Scholar
20De Bouard, A., Hayashi, N. and Saut, J.-C.. Global existence of small solutions to a relativistic nonlinear Schrödinger equation. Comm. Math. Phys. 189 (1997), 73–105.Google Scholar
21de Figueiredo, D. G., Lions, P. L. and Nussbaum, R. D.. A priori estimates and existence of positive solutions of semilinear elliptic equations. J. Math. Pures Appl. (9) 61 (1982), 41–63.Google Scholar
22De Figueiredo, D. G., Gossez, J. P. and Ubilla, P.. Local superlinearity and sublinearity for indefinite semilinear elliptic problems. J. Funct. Anal. 199 (2003), 452–467.Google Scholar
23Delgado, M. and Suárez, A.. On the existence and multiplicity of positive solutions for some indefinite nonlinear eigenvalue problem. Proc. Amer. Math. Soc. 132 (2004), 1721–1728.Google Scholar
24Del Pino, M. and Manásevich, R.. Global bifurcation from the eigenvalues of the p-Lapiacian. J. Differ. Equ. 92 (1991), 226–251.Google Scholar
25Evans, L. C.. Partial Differ. Equ. (Rhode Island: AMS, 1998).Google Scholar
26Fitzpatrick, P. M., Massabò, I. and Pejsachowicz, J.. Global several-parameter bifurcation and continuation theorems: a unified approach via complementing maps. Math. Ann. 263 (1983), 61–73.Google Scholar
27Gelfand, I. M.. Some problems in the theory of quasilinear equations. Amer. Math. Soc. Transl. Ser. 2 29 (1963), 295–381.Google Scholar
28Gidas, B. and Spruck, J.. A priori bounds for positive solutions of nonlinear elliptic equations. Comm. Partial Differ. Equ. 8 (1981), 883–901.Google Scholar
29Gilbarg, D. and Trudinger, N. S.. Elliptic partial differential equations of second order (Berlin, Heidelberg: Springer-Verlag, 2001).Google Scholar
30Hasse, R. W.. A general method for the solution of nonlinear soliton and kink Schrödinger equations. Z. Physik B 37 (1980), 83–87.Google Scholar
31Joseph, D. D. and Lundgren, T. S.. Quasilinear Dirichlet problems driven by positive sources. Arch. Rational Meth. Anal. 49 (1973), 241–269.Google Scholar
32Korman, P., Li, Y. and Ouyang, T.. Exact multiplicity results for boundary value problems with nonlinearities generalising cubic. Proc. Roy. Soc. Edinburgh Sect. A 126 (1996), 599–616.Google Scholar
33Korman, P., Li, Y. and Ouyang, T.. An exact multiplicity result for a class of semilinear equations. Comm. Partial Differ. Equ. 22 (1997), 661–684.Google Scholar
34Kosevich, A. M., Ivanov, B. A. and Kovalev, A. S.. Magnetic solitons. Phys. Rep. 194 (1990), 117–238.Google Scholar
35Kurihura, S.. Large-amplitude quasi-solitons in superfluid films. J. Phys. Soc. Japan 50 (1981), 3262–3267.Google Scholar
36Laedke, E. W., Spatschek, K. H. and Stenflo, L.. Evolution theorem for a class of perturbed envelope soliton solutions. J. Math. Phys. 24 (1983), 2764–2769.Google Scholar
37Lange, H., Toomire, B. and Zweifel, P. F.. Time-dependent dissipation in nonlinear Schrödinger systems. J. Math. Phys. 36 (1995), 1274–1283.Google Scholar
38Lange, H., Poppenberg, M. and Teismann, H.. Nash-Moser methods for the solution of quasilinear Schrödinger equations. Comm. Partial Differ. Equ. 24 (1999), 1399–1418.Google Scholar
39Lions, P. L.. Minimization problems in L 1(ℝ3). J. Funct. Anal. 41 (1981), 236–275.Google Scholar
40Lions, P. L.. On the existence of positive solutions of semilinear elliptic equations. SIAM Rev. 24 (1982), 441–467.Google Scholar
41Litvak, A. G. and Sergeev, A. M.. One dimensional collapse of plasma waves. JETP Lett. 27 (1978), 517–520.Google Scholar
42Liu, J.-Q. and Wang, Z.-Q.. Soliton solutions for quasilinear Schrödinger equations. Proc. Amer. Math. Soc. 131 (2003), 441–448.Google Scholar
43Liu, J.-Q., Wang, Y.-Q. and Wang, Z.-Q.. Soliton solutions for quasilinear Schrödinger equations, II. J. Differ. Equ. 187 (2003), 473–493.Google Scholar
44Makhankov, V. G. and Fedyanin, V. K.. Non-linear effects in quasi-one-dimensional models of condensed matter theory. Phys. Rep. 104 (1984), 1–86.Google Scholar
45Nakamura, A.. Damping and modification of exciton solitary waves. J. Phys. Soc. Japan 42 (1977), 1824–1835.Google Scholar
46Ouyang, T. and Shi, J.. Exact multiplicity of positive solutions for a class of semilinear problem. J. Differ. Equ. 146 (1998), 121–156.Google Scholar
47Ouyang, T. and Shi, J.. Exact multiplicity of positive solutions for a class of semilinear problem II. J. Differ. Equ. 158 (1999), 94–151.Google Scholar
48Poppenberg, M., Schmitt, K. and Wang, Z.-Q.. On the existence of soliton solutions to quasilinear Schrödinger equations. Calc. Var. 14 (2002), 329–344.Google Scholar
49Porkolab, M. and Goldman, M. V.. Upper hybrid solitons and oscillating two-stream instabilities. Phys. Fluids. 19 (1976), 872–881.Google Scholar
50Pucci, P. and Serrin, J.. The strong maximum principle revisited. J. Differ. Equ. 196 (2004), 1–66.Google Scholar
51Quispel, G. R. W. and Capel, H. W.. Equation of motion for the Heisenberg spin chain. Physica. A. 110 (1982), 41–80.Google Scholar
52Rabinowitz, P. H.. Some global results for nonlinear eigenvalue problems. J. Funct. Anal. 7 (1971), 487–513.Google Scholar
53Rabinowitz, P. H.. On bifurcation from infinity. J. Funct. Anal. 14 (1973), 462–475.Google Scholar
54Rabinowitz, P. H.. Variational methods for nonlinear eigenvalue problems, in Eigenvalues of non-linear problems (Rome: C.I.M.E., Ediz. Cremonese, 1974).Google Scholar
55Ritchie, B.. Relativistic self-focusing and channel formation in laser-plasma interactions. Phys. Rev. E 50 (1994), 687–689.Google Scholar
56Shi, J.. Blow up points of solution curves for a semilinear problem. Topol. Methods Nonlinear Anal. 15 (2000), 251–266.Google Scholar
57Shi, J.. Exact multiplicity of positive solutions to a superlinear problem. Electron. J. Differ. Equ. 10 (2003), 257–265.Google Scholar
58Shi, J. and Wang, J.. Morse indices and exact multiplicity of solutions to semilinear elliptic problems. Proc. Amer. Math. Soc. 127 (1999), 3685–3695.Google Scholar
59Strass, W.. Existence of solitary waves in higher dimensions. Comm. Math. Phys. 55 (1977), 149–162.Google Scholar
60Takeno, S. and Homma, S.. Classical planar Heisenberg ferromagnet, complex scalar fields and nonlinear excitations. Progr. Theoret. Physics 65 (1981), 172–189.Google Scholar
61Whyburn, G. T.. Topological analysis (Princeton: Princeton University Press, 1958).Google Scholar