Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T17:41:05.398Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotics toward the diffusion wave for a one-dimensional compressible flow through porous media

Published online by Cambridge University Press:  12 July 2007

Kenji Nishihara
Kenji Nishihara
Affiliation:
School of Political Science and Economics, Waseda University, Tokyo 169-8050, Japan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

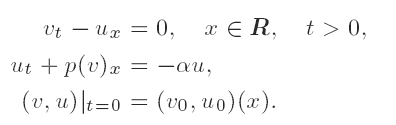Consider the Cauchy problem for a one-dimensional compressible flow through porous media, Hsiao and Liu showed that the solution (υ, u) behaves as the diffusion wave (ῡ, ū), i.e. the solution of the porous-media equation due to the Darcy law. The optimal convergence rates have been obtained by Nishihara and co-workers. When υ0(x) has the same constant state at x = ±∞, the convergence rate ‖(υ − ῡ)(·,t)‖L∞ = O(t−1) obtained is ‘optimal’, since ‖ῡ(·,t)‖∞ = O(t−1/2). However, this ‘optimal’ convergence rate is less sufficient to determine the location of the diffusion wave. Our aim in this paper is to obtain the ‘truly optimal’ convergence rate by choosing suitably located diffusion waves.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 133 , Issue 1 , February 2003 , pp. 177 - 196
Copyright
Copyright © Royal Society of Edinburgh 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)