Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-06T03:11:03.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotics for some polynomial patterns in the primes

Part of: Sequences and sets

Published online by Cambridge University Press:  17 January 2019

Pierre-Yves Bienvenu
Pierre-Yves Bienvenu*
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, UK ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove asymptotic formulae for sums of the form

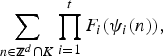$$\sum\limits_{n\in {\open z}^d\cap K} {\prod\limits_{i = 1}^t {F_i} } (\psi _i(n)),$$
where K is a convex body, each Fi is either the von Mangoldt function or the representation function of a quadratic form, and Ψ = (ψ1, …, ψt) is a system of linear forms of finite complexity. When all the functions Fi are equal to the von Mangoldt function, we recover a result of Green and Tao, while when they are all representation functions of quadratic forms, we recover a result of Matthiesen. Our formulae imply asymptotics for some polynomial patterns in the primes. For instance, they describe the asymptotic behaviour of the number of k-term arithmetic progressions of primes whose common difference is a sum of two squares.

The paper combines ingredients from the work of Green and Tao on linear equations in primes and that of Matthiesen on linear correlations amongst integers represented by a quadratic form. To make the von Mangoldt function compatible with the representation function of a quadratic form, we provide a new pseudorandom majorant for both – an average of the known majorants for each of the functions – and prove that it has the required pseudorandomness properties.

Keywords

configurations of primesprime values of polynomialsGreen-Tao method

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 5 , October 2019 , pp. 1241 - 1290
Copyright
Copyright © Royal Society of Edinburgh 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Browning, T. and Matthiesen, L.. Norm forms for arbitrary number fields as products of linear polynomials, preprint. arXiv:1307.7641, July 2013.Google Scholar
2Conlon, D., Fox, J. and Zhao, Y.. The Green-Tao theorem: an exposition. EMS Surv. Math. Sci. 1 (2014), 249–282.Google Scholar
3Erdős, P.. On the sum $\sum\nolimits_k^x { = 1d(f(k))}$. J. London Math. Soc. 27 (1952), 7–15.Google Scholar
4Fouvry, E.. Sur le problème des diviseurs de Titchmarsh. J. Reine Angew. Math. 357 (1984), 51–76.Google Scholar
5Green, B.. On arithmetic structures in dense sets of integers. Duke Math. J. 114 (2002), 215–238.Google Scholar
6Green, B. and Tao, T.. The primes contain arbitrarily long arithmetic progressions. Ann. Math. (2) 167 (2008), 481–547.Google Scholar
7Green, B. and Tao, T.. Linear equations in primes. Ann. Math. (2) 171 (2010), 1753–1850.Google Scholar
8Green, B. and Tao, T.. The Möbius function is strongly orthogonal to nilsequences. Ann. Math. (2) 175 (2012), 541–566.Google Scholar
9Green, B., Tao, T. and Ziegler, T.. An inverse theorem for the Gowers $U\sp s+1[N]$-norm. Ann. Math. (2) 176 (2012), 1231–1372.Google Scholar
10Iwaniec, H. and Kowalski, E.. Analytic number theory, vol. 53 (Providence, RI: American Mathematical Society, 2004), American Mathematical Society Colloquium Publications.Google Scholar
11Lê, T. H. and Wolf, J.. Polynomial configurations in the primes. Int. Math. Res. Not. IMRN (2014), 6448–6473.Google Scholar
12Linnik, J. V.. The dispersion method in binary additive problems. Translated by S. Schuur (Providence, RI: American Mathematical Society, 1963).Google Scholar
13Matthiesen, L.. Correlations of the divisor function. Proc. Lond. Math. Soc 104 (2012a), 827–858.Google Scholar
14Matthiesen, L.. Linear correlations amongst numbers represented by positive definite binary quadratic forms. Acta Arith 154 (2012b), 235–306.Google Scholar
15Tao, T. and Ziegler, T.. The primes contain arbitrarily long polynomial progressions. Acta Math. 201 (2008), 213–305.Google Scholar
16Tao, T. and Ziegler, T.. Narrow progressions in the primes, preprint. arXiv:1409.1327, September 2014.Google Scholar
17Tao, T. and Ziegler, T.. Polynomial patterns in the primes, preprint. arXiv:1603.07817, March 2016.Google Scholar
18Titchmarsh, E. C.. A divisor problem. Rend. di Palermo 54 (1931), 414–429.Google Scholar