Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
SNOUSSI, SEIFEDDINE
and
TAYACHI, SLIM
2001.
ASYMPTOTIC SELF-SIMILAR BEHAVIOR OF SOLUTIONS FOR A SEMILINEAR PARABOLIC SYSTEM.
Communications in Contemporary Mathematics,
Vol. 03,
Issue. 03,
p.
363.
Ben-Artzi, M.
2001.
Partial Differential Equations and Spectral Theory.
p.
7.
Ben-Artzi, Matania
Souplet, Philippe
and
Weissler, Fred B.
2002.
The local theory for viscous Hamilton–Jacobi equations in Lebesgue spaces.
Journal de Mathématiques Pures et Appliquées,
Vol. 81,
Issue. 4,
p.
343.
Ben-Artzi, M.
2002.
Nonlinear Partial Differential Equations and their Applications - Collège de France Seminar Volume XIV.
Vol. 31,
Issue. ,
p.
57.
Snoussi, Seifeddine
and
Tayachi, Slim
2002.
Global existence, asymptotic behavior and self-similar solutions for a class of semilinear parabolic systems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 48,
Issue. 1,
p.
13.
Hesaaraki, Mahmoud
and
Moameni, Abbas
2004.
Blow-up of positive solutions for a family of nonlinear parabolic equations in general domain in RN.
Michigan Mathematical Journal,
Vol. 52,
Issue. 2,
Dickstein, Flávio
2006.
Blowup stability of solutions of the nonlinear heat equation with a large life span.
Journal of Differential Equations,
Vol. 223,
Issue. 2,
p.
303.
SNOUSSI, SEIFEDDINE
and
TAYACHI, SLIM
2007.
ASYMPTOTICALLY SELF-SIMILAR GLOBAL SOLUTIONS OF A DAMPED WAVE EQUATION.
Communications in Contemporary Mathematics,
Vol. 09,
Issue. 02,
p.
253.
Filippucci, Roberta
Pucci, Patrizia
and
Rigoli, Marco
2009.
On entire solutions of degenerate elliptic differential inequalities with nonlinear gradient terms.
Journal of Mathematical Analysis and Applications,
Vol. 356,
Issue. 2,
p.
689.
Sun, Fuqin
Li, Fan
and
Jia, Xiuqing
2010.
Asymptotically self-similar global solutions for a higher-order semilinear parabolic equation.
Mathematical Methods in the Applied Sciences,
Vol. 33,
Issue. 12,
p.
1473.
Zhang, Qingshan
and
Shi, Peihu
2010.
Global solutions and self-similar solutions of semilinear parabolic equations with nonlinear gradient terms.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 72,
Issue. 6,
p.
2744.
Al Elaiw, Abeer
and
Tayachi, Slim
2012.
Different asymptotic behavior of global solutions for a parabolic system with nonlinear gradient terms.
Journal of Mathematical Analysis and Applications,
Vol. 387,
Issue. 2,
p.
970.
Cazenave, Thierry
Dickstein, Flávio
and
B. Weissler, Fred
2012.
Multi-scale multi-profile global solutions of parabolic equations in $\mathbb{R}^N $.
Discrete & Continuous Dynamical Systems - S,
Vol. 5,
Issue. 3,
p.
449.
Molinet, Luc
and
Tayachi, Slim
2015.
Remarks on the Cauchy problem for the one-dimensional quadratic (fractional) heat equation.
Journal of Functional Analysis,
Vol. 269,
Issue. 8,
p.
2305.
Hani, Houda
and
Khenissi, Moez
2015.
On a finite difference scheme for blow up solutions for the Chipot–Weissler equation.
Applied Mathematics and Computation,
Vol. 268,
Issue. ,
p.
1199.
Ben Slimene, Byrame
Tayachi, Slim
and
Weissler, Fred B.
2017.
Well-posedness, global existence and large time behavior for Hardy–Hénon parabolic equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 152,
Issue. ,
p.
116.
Fujishima, Yohei
and
Ioku, Norisuke
2018.
Existence and nonexistence of solutions for the heat equation with a superlinear source term.
Journal de Mathématiques Pures et Appliquées,
Vol. 118,
Issue. ,
p.
128.
Tayachi, Slim
and
Zaag, Hatem
2019.
Existence of a stable blow-up profile for the nonlinear heat equation with a critical power nonlinear gradient term.
Transactions of the American Mathematical Society,
Vol. 371,
Issue. 8,
p.
5899.
Zhang, Zhengce
and
Zhang, Xiangli
2019.
Asymptotic behavior of solutions for a free boundary problem with a nonlinear gradient absorption.
Calculus of Variations and Partial Differential Equations,
Vol. 58,
Issue. 1,
Gomes, Halley
and
Viana, Arlúcio
2021.
Existence, symmetries, and asymptotic properties of global solutions for a fractional diffusion equation with gradient nonlinearity.
SN Partial Differential Equations and Applications,
Vol. 2,
Issue. 1,


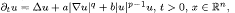 u(0) = ϧwhere
u(0) = ϧwhere 