No CrossRef data available.
Article contents
6.—On the Distribution of the Eigenvalues and the Order of the Eigenfunctions of a Fourth-order Singular Boundary Value Problem
Published online by Cambridge University Press: 14 February 2012
Synopsis
This paper is concerned with the asymptotic properties of the eigenvalues and eigenfunctions of the boundary value problem
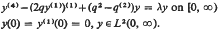
With suitable restrictions placed on the real-valued coefficient q the spectrum of this problem, with respect to the eigenvalue parameter λ, is discrete; let {λn; n = 1, 2, …} and {ψn; n = 1, 2, …} be the eigenvalues and associated eigenfunctions. Asymptotic formulae are obtained for N(λ), the number of eigenvalues not exceeding the real number λ, and for ψn(x) as n→∞ where x is a fixed, positive real number.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 71 , Issue 1 , 1972 , pp. 61 - 75
- Copyright
- Copyright © Royal Society of Edinburgh 1972


