Article contents
8.—On a Class of Series Expansions in the Theory of Emden's Equation*
Published online by Cambridge University Press: 14 February 2012
Synopsis
This paper deals with the nature of movable singularities of solutions of Emden's equation

at which the solution becomes infinite. If m = 1 + 2/p with p > 1 an integer, then the solution becomes infinite at a given point x = c as
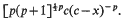
By the general theory of P. Painlevé on movable poles of solutions of non-linear second order differential equations this ‘pseudo-pole’ cannot actually be a pole of order p. Instead of a bona fide Laurent series at x = c we obtain a series expansion of the form
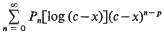
where Pn(t) is a polynomial in t of degree at most [n/(2p + 2)]. The object of this paper is to derive these series and to prove convergence for p = 2. In this case deg [P6m] is strictly equal to m. For other values of p, see Section 8, Addenda.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 71 , Issue 2 , 1973 , pp. 95 - 110
- Copyright
- Copyright © Royal Society of Edinburgh 1973
References
References to Literature
- 1
- Cited by


