Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Magnetic helicity was found important in understanding solar activities such as flares and coronal mass ejections (CME). Berger and field (1984) derived an expression for helicity flux dHm/dt, that can be applied to an individual solar active region (AR) occupying an area S of the photosphere,
(1)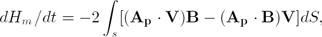 \begin{linenomath}
dH_{m}/dt=-2\int_{s}[(\mathbf{A_{p}}\cdot \mathbf{V})\mathbf{B}-(\mathbf{A_{p}} \cdot \mathbf{B})\mathbf{V}] dS, \eqno{(1)}
\end{linenomath}
\begin{linenomath}
dH_{m}/dt=-2\int_{s}[(\mathbf{A_{p}}\cdot \mathbf{V})\mathbf{B}-(\mathbf{A_{p}} \cdot \mathbf{B})\mathbf{V}] dS, \eqno{(1)}
\end{linenomath}
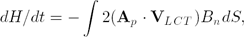 \begin{linenomath}
dH/dt=-\int2(\textbf{A}_{p}\cdot \textbf{V}_{LCT})B_{n}dS, \eqno{(2)}
\end{linenomath}
\begin{linenomath}
dH/dt=-\int2(\textbf{A}_{p}\cdot \textbf{V}_{LCT})B_{n}dS, \eqno{(2)}
\end{linenomath}
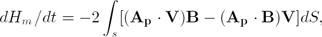 \begin{linenomath}
dH_{m}/dt=-2\int_{s}[(\mathbf{A_{p}}\cdot \mathbf{V})\mathbf{B}-(\mathbf{A_{p}} \cdot \mathbf{B})\mathbf{V}] dS, \eqno{(1)}
\end{linenomath}
\begin{linenomath}
dH_{m}/dt=-2\int_{s}[(\mathbf{A_{p}}\cdot \mathbf{V})\mathbf{B}-(\mathbf{A_{p}} \cdot \mathbf{B})\mathbf{V}] dS, \eqno{(1)}
\end{linenomath}
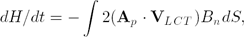 \begin{linenomath}
dH/dt=-\int2(\textbf{A}_{p}\cdot \textbf{V}_{LCT})B_{n}dS, \eqno{(2)}
\end{linenomath}
\begin{linenomath}
dH/dt=-\int2(\textbf{A}_{p}\cdot \textbf{V}_{LCT})B_{n}dS, \eqno{(2)}
\end{linenomath}