Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T00:23:15.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of INPOP planetary ephemerides and Bepi-Colombo simulations

Published online by Cambridge University Press:  30 May 2022

A. Fienga Open the ORCID record for A. Fienga [Opens in a new window] ,
L. Bigot ,
D. Mary ,
P. Deram ,
A. Di Ruscio ,
L. Bernus ,
M. Gastineau  and
J. Laskar
A. Fienga
Affiliation:
GéoAzur, Observatoire Côte d’Azur, Université Côte d’Azur, CNRS, 250 Av. A. Einstein, Valbonne, 06560, France email: [email protected] IMCCE, Observatoire de Paris, PSL University, CNRS, Sorbonne Université, 77 avenue Denfert-Rochereau, Paris, 75014, France
L. Bigot
Affiliation:
Lagrange, Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Lagrange UMR 7293, CS 34229, 06304, Nice Cedex 4, France
D. Mary
Affiliation:
Lagrange, Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Lagrange UMR 7293, CS 34229, 06304, Nice Cedex 4, France
P. Deram
Affiliation:
GéoAzur, Observatoire Côte d’Azur, Université Côte d’Azur, CNRS, 250 Av. A. Einstein, Valbonne, 06560, France email: [email protected]
A. Di Ruscio
Affiliation:
GéoAzur, Observatoire Côte d’Azur, Université Côte d’Azur, CNRS, 250 Av. A. Einstein, Valbonne, 06560, France email: [email protected] Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, via Eudossiana 18, 00184 Rome, Italy
L. Bernus
Affiliation:
GéoAzur, Observatoire Côte d’Azur, Université Côte d’Azur, CNRS, 250 Av. A. Einstein, Valbonne, 06560, France email: [email protected] IMCCE, Observatoire de Paris, PSL University, CNRS, Sorbonne Université, 77 avenue Denfert-Rochereau, Paris, 75014, France
M. Gastineau
Affiliation:
IMCCE, Observatoire de Paris, PSL University, CNRS, Sorbonne Université, 77 avenue Denfert-Rochereau, Paris, 75014, France
J. Laskar
Affiliation:
IMCCE, Observatoire de Paris, PSL University, CNRS, Sorbonne Université, 77 avenue Denfert-Rochereau, Paris, 75014, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give here a detailed description of the latest INPOP planetary ephemerides INPOP20a. We test the sensitivity of the Sun oblateness determination obtained with INPOP to different models for the Sun core rotation. We also present new evaluations of possible GRT violations with the PPN parameters β, γ and 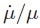. With a new method for selecting acceptable alternative ephemerides we provide conservative limits of about 7.16 × 10-5 and 7.49 × 10-5 for β-1 and γ-1 respectively using the present day planetary data samples. We also present simulations of Bepi-Colombo range tracking data and their impact on planetary ephemeris construction. We show that the use of future BC range observations should improve these estimates, in particular γ. Finally, interesting perspectives for the detection of the Sun core rotation seem to be reachable thanks to the BC mission and its accurate range measurements in the GRT frame.

Keywords

Planetary ephemeridesSpace mission trackingFundamental physicssolar physics.
Type
Research Article
Information
Proceedings of the International Astronomical Union , Volume 15 , Symposium S364: Multi-scale (Time and Mass) Dynamics of Space Objects (Oct 2021) , October 2019 , pp. 31 - 51
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of International Astronomical Union

References

Antia, H. M., Chitre, S. M., and Gough, D. O.. Temporal variations in the Sun’s rotational kinetic energy. A&A, 477(2):657–663, January 2008.Google Scholar
Appourchaux, T. and Corbard, T.. Searching for g modes. II. Unconfirmed g-mode detection in the power spectrum of the time series of round-trip travel time. A&A, 624:A106, April 2019.CrossRefGoogle Scholar
Archinal, B. A., Acton, C. H., A’Hearn, M. F., Conrad, A., Consolmagno, G. J., Duxbury, T., Hestroffer, D., Hilton, J. L., Kirk, R. L., Klioner, S. A., McCarthy, D., Meech, K., Oberst, J., Ping, J., Seidelmann, P. K., Tholen, D. J., Thomas, P. C., and Williams, I. P.. Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2015. Celestial Mechanics and Dynamical Astronomy, 130(3):22, February 2018.CrossRefGoogle Scholar
Bernus, L.. Tests de graviation à l’échelle du systeme solaire. PhD thesis, Observatoire de Paris, 2020.Google Scholar
Bernus, L., Minazzoli, O., Fienga, A., Gastineau, M., Laskar, J., and Deram, P.. Constraining the Mass of the Graviton with the Planetary Ephemeris INPOP. Phys. Rev. Lett., 123(16):161103, October 2019.CrossRefGoogle ScholarPubMed
Bernus, L., Minazzoli, O., Fienga, A., Gastineau, M., Laskar, J., Deram, P., and Di Ruscio, A.. Constraint on the Yukawa suppression of the Newtonian potential from the planetary ephemeris INPOP19a. Phys. Rev. D, 102(2):021501, July 2020.CrossRefGoogle Scholar
Bertotti, B., Iess, L., and Tortora, P.. A test of general relativity using radio links with the Cassini spacecraft. Nature, 425(6956):374–376, September 2003.CrossRefGoogle ScholarPubMed
Chaplin, W. J., Christensen-Dalsgaard, J., Elsworth, Y., Howe, R., Isaak, G. R., Larsen, R. M., New, R., Schou, J., Thompson, M. J., and Tomczyk, S.. Rotation of the solar core from BiSON and LOWL frequency observations. MNRAS, 308(2):405–414, September 1999.CrossRefGoogle Scholar
Christensen-Dalsgaard, J.. Private communication, 2021.Google Scholar
De Marchi, F. and Cascioli, G.. Testing general relativity in the solar system: present and future perspectives. Classical and Quantum Gravity, 37(9): 095007, May 2020.CrossRefGoogle Scholar
Di Mauro, M. P.. Helioseismology: A Fantastic Tool to Probe the Interior of the Sun, volume 599, pages 31–67. 2003.CrossRefGoogle Scholar
Di Ruscio, A., Fienga, A., Durante, D., Iess, L., Laskar, J., and Gastineau, M.. Analysis of Cassini radio tracking data for the construction of INPOP19a: A new estimate of the Kuiper belt mass. A&A, 640:A7, August 2020.Google Scholar
Fienga, A., Laskar, J., Morley, T., Manche, H., Kuchynka, P., Le Poncin-Lafitte, C., Budnik, F., Gastineau, M., and Somenzi, L.. INPOP08, a 4-D planetary ephemeris: from asteroid and time-scale computations to ESA Mars Express and Venus Express contributions. A&A, 507:1675–1686, December 2009.Google Scholar
Fienga, A., Laskar, J., Exertier, P., Manche, H., and Gastineau, M.. Numerical estimation of the sensitivity of INPOP planetary ephemerides to general relativity parameters. Celestial Mechanics and Dynamical Astronomy, 123: 325–349, November 2015.CrossRefGoogle Scholar
Fienga, A., Deram, P., Viswanathan, V., Di Ruscio, A., Bernus, L., Durante, D., Gastineau, M., and Laskar, J.. INPOP19a planetary ephemerides. Notes Scientifiques et Techniques de l’Institut de Mecanique Celeste, 109, December 2019.Google Scholar
Fienga, A., Avdellidou, C., and Hanuš, J.. Asteroid masses obtained with INPOP planetary ephemerides. MNRAS, 492(1):589–602, February 2020.CrossRefGoogle Scholar
Fossat, E. and Schmider, F. X.. More about solar g modes. A&A, 612:L1, April 2018.Google Scholar
Fossat, E., Boumier, P., Corbard, T., Provost, J., Salabert, D., Schmider, F. X., Gabriel, A. H., Grec, G., Renaud, C., Robillot, J. M., Roca-Cortés, T., Turck-Chièze, S., Ulrich, R. K., and Lazrek, M.. Asymptotic g modes: Evidence for a rapid rotation of the solar core. A&A, 604:A40, August 2017.Google Scholar
Garca, R. A., Corbard, T., Chaplin, W. J., Couvidat, S., Eff-Darwich, A., Jiménez-Reyes, S. J., Korzennik, S. G., Ballot, J., Boumier, P., Fossat, E., Henney, C. J., Howe, R., Lazrek, M., Lochard, J., Pallé, P. L., and Turck-Chièze, S.. About the rotation of the solar radiative interior. Sol. Phys., 220(2):269–285, April 2004.CrossRefGoogle Scholar
Garca, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., Ballot, J., Pallé, P. L., Eff-Darwich, A., Mathur, S., and Provost, J.. Tracking Solar Gravity Modes: The Dynamics of the Solar Core. Science, 316(5831):1591, June 2007.CrossRefGoogle Scholar
Gavryuseva, E., Gavryusev, V., and Di Mauro, M. P.. Rotational Split of Solar Acoustic Modes from GONG Experiment. In Korzennik, S., editor, Structure and Dynamics of the Interior of the Sun and Sun-like Stars, volume 418 of ESA Special Publication, page 193, January 1998.Google Scholar
Genova, A., Mazarico, E., Goossens, S., Lemoine, F.G., Neumann, G. A., Smith, D. E., and Zuber, M. T.. Solar system expansion and strong equivalence principle as seen by the NASA MESSENGER mission. Nature Communications, 9:289, January 2018.CrossRefGoogle ScholarPubMed
Gough, D. O.. A new measure of the solar rotation. MNRAS, 196:731–745, September 1981.CrossRefGoogle Scholar
Gough, D. O.. Some Glimpses from Helioseismology at the Dynamics of the Deep Solar Interior. Space Sci. Rev., 196(1-4):15–47, December 2015.CrossRefGoogle Scholar
Hees, A.. Private communication, 2015.Google Scholar
Iess, L., Asmar, S. W., Cappuccio, P., Cascioli, G., De Marchi, F., di Stefano, I., Genova, A., Ashby, N., Barriot, J. P., Bender, P., Benedetto, C., Border, J. S., Budnik, F., Ciarcia, S., Damour, T., Dehant, V., Di Achille, G., Di Ruscio, A., Fienga, A., Formaro, R., Klioner, S., Konopliv, A., Lematre, A., Longo, F., Mercolino, M., Mitri, G., Notaro, V., Olivieri, A., Paik, M., Palli, A., Schettino, G., Serra, D., Simone, L., Tommei, G., Tortora, P., Van Hoolst, T., Vokrouhlický, D., Watkins, M., Wu, X., and Zannoni, M.. Gravity, Geodesy and Fundamental Physics with BepiColombo’s MORE Investigation. Space Sci. Rev., 217(1):21, February 2021.CrossRefGoogle Scholar
Imperi, L. and Iess, L.. The determination of the post-Newtonian parameter g during the cruise phase of BepiColombo. Classical and Quantum Gravity, 34(7): 075002, April 2017.CrossRefGoogle Scholar
Imperi, L., Iess, L., and Mariani, M. J.. An analysis of the geodesy and relativity experiments of BepiColombo. Icarus, 301:9025, February 2018.CrossRefGoogle Scholar
Katoch, S. and S..S. Chauhan. A review on genetic algorithm: past, present, and future. Multimedia Tools and Applications, 80(5): 8091–8126, February 2021.CrossRefGoogle ScholarPubMed
Komm, R., Howe, R., Durney, B. R., and Hill, F.. Temporal Variation of Angular Momentum in the Solar Convection Zone. ApJ, 586(1):650–662, March 2003.CrossRefGoogle Scholar
Lazrek, M., Pantel, A., Fossat, E., Gelly, B., Schmider, F. X., Fierry-Fraillon, D., Grec, G., Loudagh, S., Ehgamberdiev, S., Khamitov, I., Hoeksema, J. T., Pallé, P. L., and Régulo, C.. Is the Solar Core Rotating Faster of Slower Than the Envelope? Sol. Phys., 166(1):1–16, June 1996.CrossRefGoogle Scholar
Lense, J. and Thirring, H.. Über den Einfluß der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Physikalische Zeitschrift, 19:156, January 1918.Google Scholar
Moskovitz, N., Schottland, R., Burt, B., Bailen, M., and Wasserman, L.. astorb at Lowell Observatory: A comprehensive system to enable asteroid science. In AAS/Division for Planetary Sciences Meeting Abstracts #50, volume 50 of AAS/Division for Planetary Sciences Meeting Abstracts, page 408.08, October 2018.Google Scholar
Moyer, T.D.. Formulation for observed and computed values of deep space network data types for navigation. Monography of DEEP SPACE COMMUNICATIONS AND NAVIGATION Series 2, JPL, 2000.Google Scholar
Park, R. S., Folkner, W. M., Konopliv, A. S., Williams, J. G., Smith, D. E., and Zuber, M. T.. Precession of Mercury’s Perihelion from Ranging to the MESSENGER Spacecraft. AJ, 153:121, March 2017.CrossRefGoogle Scholar
Pijpers, F. P.. Helioseismic determination of the solar gravitational quadrupole moment. MNRAS, 297(3):L76–L80, July 1998.CrossRefGoogle Scholar
Roca Cortés, T., Lazrek, M., Bertello, L., Thiery, S., Baudin, F., Garcia, R. A., and Team, GOLF. The Solar Acoustic Spectrum as Seen by GOLF. III. Asymmetries, Resonant Frequencies and Splittings. In Korzennik, S., editor, Structure and Dynamics of the Interior of the Sun and Sun-like Stars, volume 418 of ESA Special Publication, page 329, January 1998.Google Scholar
Roxburgh, I. W.. Gravitational multipole moments of the Sun determined from helioseismic estimates of the internal structure and rotation. A&A, 377:688–690, October 2001.Google Scholar
Scherrer, P. H. and Gough, D. O.. A Critical Evaluation of Recent Claims Concerning Solar Rotation. ApJ, 877(1):42, May 2019.CrossRefGoogle Scholar
Hannah Schunker, Jesper Schou, Gaulme, Patrick, and Gizon, Laurent. Fragile Detection of Solar g-Modes by Fossat et al. Sol. Phys., 293(6):95, June 2018.CrossRefGoogle Scholar
Soffel, M. and Frutos, F.. On the usefulness of relativistic space-times for the description of the Earth’s gravitational field. Journal of Geodesy, 90(12):1345–1357, December 2016.CrossRefGoogle Scholar
Standish, E.M.. The jpl de405 planetary and lunar ephemerides. 2001.Google Scholar
Thompson, M. J., Christensen-Dalsgaard, J., Miesch, M. S., and Toomre, J.. The Internal Rotation of the Sun. ARA&A, 41:599–643, January 2003.Google Scholar
Thor, R. N., Kallenbach, R., Christensen, U. R., Stark, A., Steinbrügge, G., Di Ruscio, A., Cappuccio, P., Iess, L., Hussmann, H., and Oberst, J.. Prospects for measuring mercurys tidal love number h2 with the bepicolombo laser altimeter. A&A, 633:A85, 2020. URL https://doi.org/10.1051/0004-6361/201936517.Google Scholar