Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T15:56:24.229Z Has data issue: false hasContentIssue false
  • English
  • Français

1/1 resonant periodic orbits in three dimensional planetary systems

Published online by Cambridge University Press:  05 January 2015

Kyriaki I. Antoniadou ,
George Voyatzis  and
Harry Varvoglis
Kyriaki I. Antoniadou*
Affiliation:
Sect. of Astrophysics, Astronomy and Mechanics, Dept. of Physics, Aristotle University of Thessaloniki, 54124, Greece
George Voyatzis*
Affiliation:
Sect. of Astrophysics, Astronomy and Mechanics, Dept. of Physics, Aristotle University of Thessaloniki, 54124, Greece
Harry Varvoglis*
Affiliation:
Sect. of Astrophysics, Astronomy and Mechanics, Dept. of Physics, Aristotle University of Thessaloniki, 54124, Greece
*
1email: [email protected]
2email: [email protected]
3email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the dynamics of a two-planet system, which evolves being in a 1/1 mean motion resonance (co-orbital motion) with non-zero mutual inclination. In particular, we examine the existence of bifurcations of periodic orbits from the planar to the spatial case. We find that such bifurcations exist only for planetary mass ratios 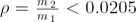$\rho=\frac{m_2}{m_1}<0.0205$. For ρ in the interval 0<ρ<0.0205, we compute the generated families of spatial periodic orbits and their linear stability. These spatial families form bridges, which start and end at the same planar family. Along them the mutual planetary inclination varies. We construct maps of dynamical stability and show the existence of regions of regular orbits in phase space.

Keywords

celestial mechanicsco-orbital motionspatial periodic orbitsplanetary systems
Type
Contributed Papers
Information
Proceedings of the International Astronomical Union , Volume 9 , Issue S310: Complex Planetary Systems , July 2014 , pp. 82 - 83
Copyright
Copyright © International Astronomical Union 2014 

References

Antoniadou, K. I. & Voyatzis, G. 2014, Ap&SS, 349, 657Google Scholar
Hadjidemetriou, J. D., Psychoyos, D., & Voyatzis, G. 2009, Cel. Mech. Dyn. Astron., 104, 23CrossRefGoogle Scholar
Hadjidemetriou, J. D. & Voyatzis, G. 2011, Cel. Mech. Dyn. Astron., 111, 179Google Scholar
Robutel, P. & Pousse, A. 2013, Cel. Mech. Dyn. Astron., 117, 17Google Scholar
Voyatzis, G. 2008, ApJ, 675, 802Google Scholar