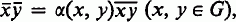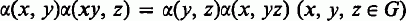Research Article
Genetic algebras associated with sex linkage
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 113-120
-
- Article
-
- You have access
- Export citation
In what spaces is every closed normal cone regular?
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 121-125
-
- Article
-
- You have access
- Export citation
Embedding topological semigroups in topological groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 127-138
-
- Article
-
- You have access
- Export citation
A generalisation of the Erdélyi-Kober operators
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 139-148
-
- Article
-
- You have access
- Export citation
A nonembedding result for complex Grassmann manifolds
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 149-153
-
- Article
-
- You have access
- Export citation
Mean value properties of generalised eigenfunctions†
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 155-158
-
- Article
-
- You have access
- Export citation
On a generalisation of monotonic sequences
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 159-164
-
- Article
-
- You have access
- Export citation
The radical of the group algebra of a sub-group, of a polycyclic group and of a restricted SN-group
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 165-171
-
- Article
-
- You have access
- Export citation
On commutative V*-algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 173-180
-
- Article
-
- You have access
- Export citation
On asymptotically stable sets
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 181-186
-
- Article
-
- You have access
- Export citation
On elemental annihilator rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 187-188
-
- Article
-
- You have access
- Export citation
Book Reviews
G. H. Hardy, Collected Papers, Vol. III (Clarendon Press: Oxford University Press, 1969), 748 pp., 105s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 189-191
-
- Article
-
- You have access
- Export citation
G. H. Hardy. Collected Papers, including joint papers with J. E. Littlewood and others. Vol. IV. Edited by a Committee appointed by the London Mathematical Society. (Clarendon Press; Oxford University Press, 1969), 722 pp, 120s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 191-192
-
- Article
-
- You have access
- Export citation
John C. Clegg , Calculus of Variations (University Mathematical Texts Series, Oliver and Boyd, 1968), ix + 90 pp., 21s. (Paper bound), 27s. 6d. (cloth bound).
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 192
-
- Article
-
- You have access
- Export citation
G. Polya, Patterns of Plausible Inference (Second Edition, Princeton University Press, 1968), x + 225 pp, 72s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 192
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 17 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 17 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

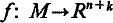 of a differentiable
of a differentiable 
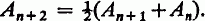
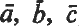 , …; a multiplication is defined on this basis of
, …; a multiplication is defined on this basis of