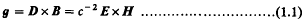Research Article
The Angular Momentum of an Electromagnetic Field
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 171-176
-
- Article
-
- You have access
- Export citation
Asymptotic Representation of Certain Real Integrals with Parameter-dependent Limits of Integration
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 177-187
-
- Article
-
- You have access
- Export citation
Combinantal Forms of a Quadric Net Applied to Irreducible Concomitant Systems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 189-195
-
- Article
-
- You have access
- Export citation
The Complete Irreducible System of Invariants of Three Quadrics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 197-204
-
- Article
-
- You have access
- Export citation
On an Integral in the Distribution of Eigenvalues
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 205-208
-
- Article
-
- You have access
- Export citation
On Measure of Sumsets: III. The Continuous (α+β)-theorem
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 209-211
-
- Article
-
- You have access
- Export citation
The Solution of Certain Dual Integral Equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 213-216
-
- Article
-
- You have access
- Export citation
Book Review
E. Landau, Grundlagen der Analysis (Chelsea Publishing Company, 3rd edition, 1960), 173 pp., $1.95.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 217
-
- Article
-
- You have access
- Export citation
N. Bourbaki Éléments d'Histoire des Mathématiques (Hermann, Paris, 1960), 276 pp., 18 NF.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 217
-
- Article
-
- You have access
- Export citation
P. G. Guest, Numerical Methods of Curve Fitting (Cambridge University Press, 1961), xiv + 422 pp., 80s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 218
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 12 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 12 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. b1-b7
-
- Article
-
- You have access
- Export citation