Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-15T18:57:59.255Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero-one law of orbital limit points for weighted shifts

Part of: Special classes of linear operators General theory of linear operators Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  07 April 2025

Antonio Bonilla ,
Rodrigo Cardeccia ,
Karl-G. Grosse-Erdmann Open the ORCID record for Karl-G. Grosse-Erdmann [Opens in a new window]  and
Santiago Muro
Antonio Bonilla
Affiliation:
Departamento de Análisis Matemático and Instituto de Matemáticas y Aplicaciones (IMAULL), Universidad de La Laguna, C/Astrofísico Francisco Sánchez, s/n, La Laguna, Tenerife, Spain
Rodrigo Cardeccia
Affiliation:
Departamento de Matemática, Instituto Balseiro, Universidad Nacional de Cuyo – C.N.E.A. and CONICET, San Carlos de Bariloche, Río Negro, Argentina
Karl-G. Grosse-Erdmann*
Affiliation:
Département de Mathématique, Université de Mons, 20 Place du Parc, Mons, Hainaut, Belgium
Santiago Muro
Affiliation:
FCEIA, Universidad Nacional de Rosario and CIFASIS, CONICET, Rosario, Santa Fe, Argentina
*
Corresponding author: Karl-G. Grosse-Erdmann, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Chan and Seceleanu have shown that if a weighted shift operator on 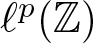$\ell^p(\mathbb{Z})$, 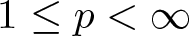$1\leq p \lt \infty$, admits an orbit with a non-zero limit point then it is hypercyclic. We present a new proof of this result that allows to extend it to very general sequence spaces. In a similar vein, we show that, in many sequence spaces, a weighted shift with a non-zero weakly sequentially recurrent vector has a dense set of such vectors, but an example on 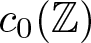$c_0(\mathbb{Z})$ shows that such an operator is not necessarily hypercyclic. On the other hand, we obtain that weakly sequentially hypercyclic weighted shifts are hypercyclic. Chan and Seceleanu have, moreover, shown that if an adjoint multiplication operator on a Bergman space admits an orbit with a non-zero limit point then it is hypercyclic. We extend this result to very general spaces of analytic functions, including the Hardy spaces.

Keywords

orbital limit pointweighted shift operatoradjoint multiplication operatorhypercyclic operatorrecurrent operator

MSC classification

Primary: 47A16: Cyclic vectors, hypercyclic and chaotic operators
Secondary: 46B45: Banach sequence spaces 47B37: Operators on special spaces (weighted shifts, operators on sequence spaces, etc.)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 34
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abakumov, E., and Abbar, A., Orbits of the backward shifts with limit points, J. Math. Anal. Appl. 537(2): (2024), , pp. 21.Google Scholar
Albiac, F. and Kalton, N. J., Topics in Banach Space Theory (Springer, New York, 2006).Google Scholar
Amouch, M., Bachir, A., Benchiheb, O., and Mecheri, S., Weakly recurrent operators, Mediterr. J. Math. 20(3): (2023), pp. 16.CrossRefGoogle Scholar
Ansari, S. I., and Bourdon, P. S., Some properties of cyclic operators, Acta Sci. Math. 63(1-2): (1997), 195–207.Google Scholar
Bayart, F., and Matheron, É., Dynamics of Linear Operators (Cambridge University Press, Cambridge, 2009).CrossRefGoogle Scholar
Bernardes, N. C., Bonilla, A., Müller, V., and Peris, A., Li-Yorke chaos in linear dynamics, Ergod. Theory Dyn. Syst. 35(6): (2015), 1723–1745.CrossRefGoogle Scholar
Bès, J., Chan, K. C., and Sanders, R., Every weakly sequentially hypercyclic shift is norm hypercyclic, Math. Proc. R. Ir. Acad. 105A(2): (2005), 79–85.CrossRefGoogle Scholar
Bonilla, A., Grosse-Erdmann, K.-G., López-Martínez, A., and Peris, A., Frequently recurrent operators, J. Funct. Anal. 283(12): (2022), pp. 36.CrossRefGoogle Scholar
Bourdon, P. S., and Feldman, N. S., Somewhere dense orbits are everywhere dense, Indiana Univ. Math. J. 52(3): (2003), 811–819.CrossRefGoogle Scholar
Cardeccia, R., and Muro, S., Multiple recurrence and hypercyclicity, Math. Scand. 128(3): (2022), 589–610.CrossRefGoogle Scholar
Cardeccia, R., and Muro, S., Frequently recurrence properties and block families. To appear in: Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM. arXiv:2204.13542, 2022.Google Scholar
Chan, K. C., The testing ground of weighted shift operators for hypercyclicity. Topological Dynamics and Topological Data Analysis (Devaney, R. L., Chan, K. C., Kumar, P. B. Vinod), (Springer, Singapore, 2021).Google Scholar
Chan, K. C., and Sanders, R., A weakly hypercyclic operator that is not norm hypercyclic, J. Operator Theory 52(1): (2004), 39–59.Google Scholar
Chan, K. C., and Seceleanu, I., Orbital limit points and hypercyclicity of operators on analytic function spaces, Math. Proc. R. Ir. Acad. 110A(1): (2010), 99–109.CrossRefGoogle Scholar
Chan, K., and Seceleanu, I., Hypercyclicity of shifts as a zero-one law of orbital limit points, J. Operator Theory 67(1): (2012), 257–277.Google Scholar
Chan, K., and Seceleanu, I., Cyclicity of vectors with orbital limit points for backward shifts, Integral Equations Operator Theory 78(2): (2014), 225–232.CrossRefGoogle Scholar
Costakis, G., Manoussos, A., and Parissis, I., Recurrent linear operators, Complex Anal. Oper. Theory 8(8): (2014), 1601–1643.CrossRefGoogle Scholar
Costakis, G., and Parissis, I., Szemerédi’s theorem, frequent hypercyclicity and multiple recurrence, Math. Scand. 110(2): (2012), 251–272.CrossRefGoogle Scholar
Godefroy, G., and Shapiro, J. H., Operators with dense, invariant, cyclic vector manifolds, J. Funct. Anal. 98(2): (1991), 229–269.CrossRefGoogle Scholar
Grivaux, S. and López-Martínez, A., Recurrence properties for linear dynamical systems: an approach via invariant measures, J. Math. Pures Appl. 169 (2023), 155–188.CrossRefGoogle Scholar
Grivaux, S., López-Martínez, A., and Peris, A., Questions in linear recurrence I: The $T\oplus T$-problem, Anal. Math. Phys. 15(1): (2025) pp. 26.Google Scholar
Grosse-Erdmann, K.-G., Hypercyclic and chaotic weighted shifts, Studia Math. 139(1): (2000), 47–68.CrossRefGoogle Scholar
Grosse-Erdmann, K.-G. and Peris Manguillot, A., Linear Chaos (Springer, London, 2011).CrossRefGoogle Scholar
He, S., Huang, Y., and Yin, Z., J $^\mathcal{F}$-class weighted backward shifts, Int. J. Bifur. Chaos Appl. Sci. Engrg. 28(6): (2018), pp. 11.CrossRefGoogle Scholar
Kalton, N. J., Peck, N. T. and Roberts, J. W., An F-Space Sampler (Cambridge University Press, Cambridge, 1984).CrossRefGoogle Scholar
Meise, R. and Vogt, D., Introduction to Functional Analysis (The Clarendon Press, Oxford University Press, New York, 1997).CrossRefGoogle Scholar
Rong, Z., The dynamic behavior of conjugate multipliers on some reflexive Banach spaces of analytic functions, Contemp. Math. 5(1): (2024), 519–526.CrossRefGoogle Scholar
Seceleanu, I., Hypercyclic operators and their orbital limit points. PhD Thesis, Bowling Green State University, 2010.Google Scholar
Shkarin, S., Non-sequential weak supercyclicity and hypercyclicity, J. Funct. Anal. 242(1): (2007), 37–77.CrossRefGoogle Scholar
Shkarin, S., Orbits of coanalytic Toeplitz operators and weak hypercyclicity. arXiv:1210.3191, 2012.Google Scholar
Singer, I., Bases in Banach Spaces. I (Springer, New York-Berlin, 1970).CrossRefGoogle Scholar