No CrossRef data available.
Article contents
Which states can be reached from a given state by unital completely positive maps?
Published online by Cambridge University Press: 05 July 2022
Abstract
For a state $\omega$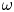 on a C$^{*}$
on a C$^{*}$ -algebra $A$
-algebra $A$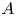 , we characterize all states $\rho$
, we characterize all states $\rho$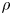 in the weak* closure of the set of all states of the form $\omega \circ \varphi$
in the weak* closure of the set of all states of the form $\omega \circ \varphi$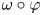 , where $\varphi$
, where $\varphi$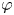 is a map on $A$
is a map on $A$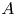 of the form $\varphi (x)=\sum \nolimits _{i=1}^{n}a_i^{*}xa_i,$
of the form $\varphi (x)=\sum \nolimits _{i=1}^{n}a_i^{*}xa_i,$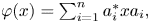 $\sum \nolimits _{i=1}^{n}a_i^{*}a_i=1$
$\sum \nolimits _{i=1}^{n}a_i^{*}a_i=1$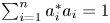 ($a_i\in A$
($a_i\in A$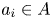 , $n\in \mathbb {N}$
, $n\in \mathbb {N}$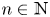 ). These are precisely the states $\rho$
). These are precisely the states $\rho$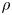 that satisfy $\|\rho |J\|\leq \|\omega |J\|$
that satisfy $\|\rho |J\|\leq \|\omega |J\|$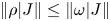 for each ideal $J$
for each ideal $J$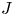 of $A$
of $A$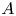 . The corresponding question for normal states on a von Neumann algebra $\mathcal {R}$
. The corresponding question for normal states on a von Neumann algebra $\mathcal {R}$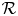 (with the weak* closure replaced by the norm closure) is also considered. All normal states of the form $\omega \circ \psi$
(with the weak* closure replaced by the norm closure) is also considered. All normal states of the form $\omega \circ \psi$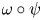 , where $\psi$
, where $\psi$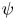 is a quantum channel on $\mathcal {R}$
is a quantum channel on $\mathcal {R}$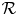 (that is, a map of the form $\psi (x)=\sum \nolimits _ja_j^{*}xa_j$
(that is, a map of the form $\psi (x)=\sum \nolimits _ja_j^{*}xa_j$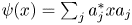 , where $a_j\in \mathcal {R}$
, where $a_j\in \mathcal {R}$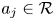 are such that the sum $\sum \nolimits _ja_j^{*}a_j$
are such that the sum $\sum \nolimits _ja_j^{*}a_j$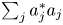 converge to $1$
converge to $1$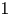 in the weak operator topology) are characterized. A variant of this topic for hermitian functionals instead of states is investigated. Maximally mixed states are shown to vanish on the strong radical of a C$^{*}$
in the weak operator topology) are characterized. A variant of this topic for hermitian functionals instead of states is investigated. Maximally mixed states are shown to vanish on the strong radical of a C$^{*}$ -algebra and for properly infinite von Neumann algebras the converse also holds.
-algebra and for properly infinite von Neumann algebras the converse also holds.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 3 , August 2022 , pp. 632 - 651
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society



