Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T21:06:33.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted estimates for the Calderón commutator

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  23 September 2019

Jiecheng Chen  and
Guoen Hu
Jiecheng Chen
Affiliation:
Department of Mathematics, Zhejiang Normal University, Jinhua321004, People's Republic of China ([email protected])
Guoen Hu
Affiliation:
Department of Applied Mathematics, Zhengzhou Information Science and Technology Institute, Zhengzhou450001, People's Republic of China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper the authors consider the weighted estimates for the Calderón commutator defined by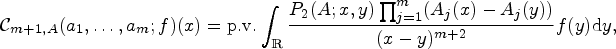

\mathcal{C}_{m+1, A}(a_1,\ldots,a_{m};f)(x)={\rm p. v.} \displaystyle\int_{\mathbb{R}}\displaystyle\frac{P_2(A; x, y)\prod\nolimits_{j=1}^m(A_j(x)-A_j(y))}{(x-y)^{m+2}}f(y){\rm d}y,
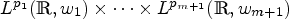with P2(A;x, y) = A(x) − A(y) − A′(y)(x − y) and A′ ∈ BMO(ℝ). Dominating this operator by multi(sub)linear sparse operators, the authors establish the weighted bounds from $L^{p_1}(\mathbb {R},w_1) \times \cdots \times L^{p_{m+1}}(\mathbb {R},w_{m+1})$ to 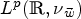$L^{p}(\mathbb {R},\nu _{\vec {\kern 1pt w}})$, with p1, …, pm+1 ∈ (1, ∞), 1/p = 1/p1 + · · · + 1/pm+1, and 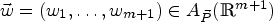$\vec {\kern 1pt w}=(w_1, \ldots , w_{m+1})\in A_{\vec {P}}(\mathbb {R}^{m+1})$. The authors also obtain the weighted weak type endpoint estimates for 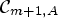$\mathcal {C}_{m+1, A}$.

Keywords

Calderón commutatorweighted inequalitymultilinear singular integral operatorsparse operatormultiple weight

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 1 , February 2020 , pp. 169 - 192
Copyright
Copyright © Edinburgh Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Buckley, S. M., Estimates for operator norms on weighted spaces and reverse Jensen inequalities, Trans. Amer. Math. Soc. 340 (1993), 253–272.CrossRefGoogle Scholar
2.Calderón, A. P., Commutators of singular integral operators, Proc. Nat. Acad. Sci. USA 53 (1965), 1092–1099.10.1073/pnas.53.5.1092CrossRefGoogle ScholarPubMed
3.Calderón, C. P., On commutators of singular integrals, Studia Math. 53 (1975), 139–174.CrossRefGoogle Scholar
4.Chen, J. and Hu, G., Weighted vector-valued bounds for a class of multilinear singular integral operators and applications, J. Korean Math. Soc. 55 (2018), 671–694.Google Scholar
5.Cohen, J., A sharp estimate for a multilinear singular integral on ℝn, Indiana Univ. Math. J. 30 (1981), 693–702.CrossRefGoogle Scholar
6.Duong, X., Gong, R., Grafakos, L., Li, J. and Yan, L., Maximal operator for multilinear singular integrals with non-smooth kernels, Indiana Univ. Math. J. 58 (2009), 2517–2542.CrossRefGoogle Scholar
7.Duong, X., Grafakos, L. and Yan, L., Multilinear operators with non-smooth kernels and commutators of singular integrals, Trans. Amer. Math. Soc. 362 (2010), 2089–2113.CrossRefGoogle Scholar
8.Duong, X. T. and McIntosh, A., Singular integral operators with nonsmooth kernels on irregular domains, Rev. Mat. Iberoamericana 15 (1999), 233–265.CrossRefGoogle Scholar
9.Grafakos, L., Modern Fourier analysis, 2nd edn (Springer, New York, 2008).Google Scholar
10.Grafakos, L., Liu, L. and Yang, D., Multilple-weighted norm inequalities for maximal singular integrals with non-smooth kernels, Proc. Royal Soc. Edinb. 141A (2011), 755–775.CrossRefGoogle Scholar
11.Hofmann, S., On certain non-standard Calderón–Zygmund operators, Studia Math. 109 (1994), 105–131.10.4064/sm-109-2-105-131CrossRefGoogle Scholar
12.Hu, G., Weighted vector-valued estimates for a non-standard Calderón–Zygmund operator, Nonlinear Anal. 165 (2017), 143–162.10.1016/j.na.2017.09.013CrossRefGoogle Scholar
13.Hu, G. and Li, D., A Cotlar type inequality for the multilinear singular integral operators and its applications, J. Math. Anal. Appl. 290 (2004), 639–653.CrossRefGoogle Scholar
14.Hu, G. and Yang, D., Sharp function estimates and weighted norm inequalities for multilinear singular integral operators, Bull. London Math. Soc. 35 (2003), 759–769.CrossRefGoogle Scholar
15.Hu, G., Yang, D. and Yang, D., Boundedness of maximal singular integral operators on spaces of homogeneous type and its applications, J. Math. Soc. Japan 59 (2007), 323–349.CrossRefGoogle Scholar
16.Hu, G. and Zhu, Y., Weighted norm inequalities with general weights for the commutator of Calderón, Acta Math. Sinica, English Ser. 29 (2013), 505–514.CrossRefGoogle Scholar
17.Hytönen, T., The sharp weighted bound for general Calderón–Zygmund operators, Ann. Math. 175 (2012), 1473–1506.CrossRefGoogle Scholar
18.Hytönen, T., Lacey, M. T. and Pérez, C., Sharp weighted bounds for the q-variation of singular integrals, Bull. Lond. Math. Soc. 45 (2013), 529–540.CrossRefGoogle Scholar
19.Hytönen, T. and Pérez, C., The L(log L)ε endpoint estimate for maximal singular integral operators, J. Math. Anal. Appl. 428 (2015), 605–626.CrossRefGoogle Scholar
20.John, F., Quasi-isometric mappings, in Seminari 1962/63 Anal. Alg. Geom. e Topol., Ist. Naz. Alta Mat., Volume 2, pp. 462–473 (Edizioni Cremonese, Rome, 1965).Google Scholar
21.Lerner, A. K., On pointwise estimate involving sparse operator, New York J. Math. 22 (2016), 341–349.Google Scholar
22.Lerner, A. K. and Nazarov, F., Intuitive dyadic calculus: The basics, Expo. Math., in press.Google Scholar
23.Lerner, A., Ombrossi, S., Pérez, C., Torres, R. H. and Trojillo–Gonzalez, R., New maximal functions and multiple weights for the multilinear Calderón–Zygmund theory, Adv. Math. 220 (2009), 1222–1264.CrossRefGoogle Scholar
24.Lerner, A. K., Obmrosi, S. and Rivera–Rios, I., On pointwise and weighted estimates for commutators of Calderón–Zygmund operators, Adv. Math. 319 (2017), 153–181.CrossRefGoogle Scholar
25.Li, K., Sparse domination theorem for multilinear singular integral operators with L r-Hörmander condition, Michigan Math. J. 67 (2018), 253–265.CrossRefGoogle Scholar
26.Li, K., Moen, K. and Sun, W., The sharp weighted bound for multilinear maximal functions and Calderón–Zygmund operators, J. Four. Anal. Appl. 20 (2014), 751–765.CrossRefGoogle Scholar
27.Petermichl, S., The sharp weighted bound for the Riesz transforms, Proc. Amer. Math. Soc. 136 (2008), 1237–1249.10.1090/S0002-9939-07-08934-4CrossRefGoogle Scholar
28.Rao, M. and Ren, Z., Theory of Orlicz spaces, Monographs and Textbooks in Pure and Applied Mathematics, Volume 146 (Marcel Dekker, New York, 1991).Google Scholar
29.Sawyer, E., Norm inequalities relating singular integrals and the maximal function, Studia Math. 75 (1983), 253–263.CrossRefGoogle Scholar
30.Strömberg, J. O., Bounded mean oscillation with Orlicz norms and duality of Hardy spaces, Indiana Univ. Math. J. 28 (1979), 511–544.CrossRefGoogle Scholar