Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lau, A.T.-M.
and
Loy, R.J.
1997.
Weak Amenability of Banach Algebras on Locally Compact Groups.
Journal of Functional Analysis,
Vol. 145,
Issue. 1,
p.
175.
Zhang, Yong
2002.
Weak amenability of module extensions of Banach algebras.
Transactions of the American Mathematical Society,
Vol. 354,
Issue. 10,
p.
4131.
Pourabbas, A.
2003.
Higher Dimensional Cohomology of Weighted Sequence Algebras.
Journal of the Australian Mathematical Society,
Vol. 75,
Issue. 1,
p.
57.
Gorgi, M. E.
and
Yazdanpanah, T.
2004.
Derivations into duals of ideals of Banach algebras.
Proceedings Mathematical Sciences,
Vol. 114,
Issue. 4,
p.
399.
Choi, Yemon
and
Ghandehari, Mahya
2014.
Weak and cyclic amenability for Fourier algebras of connected Lie groups.
Journal of Functional Analysis,
Vol. 266,
Issue. 11,
p.
6501.
ABTAHI, F.
and
GHAFARPANAH, A.
2015.
A NOTE ON CYCLIC AMENABILITY OF THE LAU PRODUCT OF BANACH ALGEBRAS DEFINED BY A BANACH ALGEBRA MORPHISM.
Bulletin of the Australian Mathematical Society,
Vol. 92,
Issue. 2,
p.
282.
Shojaee, Behrouz
and
Bodaghi, Abasalt
2015.
A Generalization of Cyclic Amenability of Banach Algebras.
Mathematica Slovaca,
Vol. 65,
Issue. 3,
p.
633.
Javanshiri, Hossein
2016.
Approximate Cyclic Amenability of $T$-Lau Product of Banach Algebras.
Taiwanese Journal of Mathematics,
Vol. 20,
Issue. 5,
Javanshiri, Hossein
and
Nemati, Mehdi
2018.
Amalgamated duplication of the Banach algebra 𝔄 along a 𝔄-bimodule 𝒜.
Journal of Algebra and Its Applications,
Vol. 17,
Issue. 09,
p.
1850169.
Ramezanpour, Mohammad
2018.
More on cyclic amenability of the Lau product of Banach algebras defined by a Banach algebra morphism.
Mathematica Slovaca,
Vol. 68,
Issue. 1,
p.
147.
Teymouri, Akram
Bodaghi, Abasalt
and
Bagha, Davood Ebrahimi
2019.
Derivations into annihilators of the ideals of Banach algebras.
Demonstratio Mathematica,
Vol. 52,
Issue. 1,
p.
20.
Alaminos, J.
Brešar, M.
Extremera, J.
and
Villena, A.R.
2019.
Zero Lie product determined Banach algebras, II.
Journal of Mathematical Analysis and Applications,
Vol. 474,
Issue. 2,
p.
1498.
Brešar, Matej
2021.
Zero Product Determined Algebras.
p.
95.
Ebadian, Ali
Jabbari, Ali
and
Shams, Saeid
2022.
On Banach algebras defined by multipliers.
Filomat,
Vol. 36,
Issue. 17,
p.
5945.
Bodaghi, Abasat
and
Valaei, Mohammad
2024.
Diagonals of Lau product Banach algebras.
Journal of Algebra and Its Applications,
Vol. 23,
Issue. 03,


 where ℱ is a Banach algebraic free product of two Banach algebras
where ℱ is a Banach algebraic free product of two Banach algebras 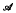 and ℬ. It follows that cyclic amenability is preserved under the formation of free products.
and ℬ. It follows that cyclic amenability is preserved under the formation of free products.