Article contents
Useful Theorems on Commutative Non-associative Algebras
Published online by Cambridge University Press: 20 January 2009
Extract
Recently J. M. Osborn has investigated the structure of a simple commutative non-associative algebra with unity element satisfying a polynomial identity, (4), (5) and (6). From his work it seems likely that if such an algebra is of degree three or more it is necessarily power-associative. In (4) he establishes a hierarchy of identities with the property that each identity is satisfied by an algebra satisfying no preceding identity. Following (5), (6),the next identity to consider is
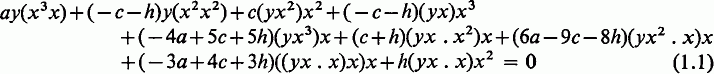
where a, c and h are elements of the ground field.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1967
References
REFERENCES
- 1
- Cited by


