No CrossRef data available.
Article contents
The Use of Green's Functions in the Mathematical Theory of the Conduction of Heat
Published online by Cambridge University Press: 20 January 2009
Extract
The use of Green's Functions in the Theory of Potential is well known. The function is most conveniently defined, for the closed surface S, as the potential which vanishes over S and is infinite as 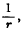 when r is zero, at the point P(x0, y0, z0), inside the surface. If this is represented by G(P), the solution with no infinity inside S and an arbitrary value V over the surface, is given by
when r is zero, at the point P(x0, y0, z0), inside the surface. If this is represented by G(P), the solution with no infinity inside S and an arbitrary value V over the surface, is given by
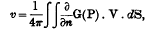
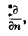 denoting differentiation along the outward drawn normal.
denoting differentiation along the outward drawn normal.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1902
References
page 41 note * Cf. Pockels. Über die Partielle Differential-gleichung ![]() Theil IV. § 4. Leipzig 1891.
Theil IV. § 4. Leipzig 1891.
Schwarzschild. Die Beugung und Polarization des Lichts durch einen Spalt. Math. Ann. Bd. 55. 1902.
page 44 note * Minnigerode. Uber die Wärme-Leitung in Krystallen. Diss. Göttingen. 1862.
page 44 note † Betti.
(1) Sopra la determinazione delta lemperatura variabile diun cylindro. Annali delle University Toscane. Tom. I. 1867.
(2) Sopra la determinazione delle temperatura variabile di Una lastra terminata. Annali di Matematica. Tom. I. 1867.
(3) Sopra la determinazione delle temperatura net corpi solidi ed omogenii. Mem. della Soc. Italiana delle Sciauze. Ser. III. Tom. I. 1868.
(4) Sopra la propagazione del calore. Chelini Collezione 1881.
Sommerfeld. Zur Analytische Thtorie der Warme-Leitung. Math. Ann. Bd. 45. 1894.
Weber-Riemann. Die Partiellen Differential-gleichungen der PhysiL Bd. II., § 51. 1901.
page 45 note * Hobson. Synthetical Solutions in the Conduction of Heat. Proc. Lond. Math. Soc. Vol. XIX. 1888.
page 45 note † Dougall. (i) The Determination of Green's Function by means of Cylindrical or Spherical Harmonics. Proc. Edin. Math. Soc. Vol. XVIII. 1900.
(ii) Note on the Application of Complex Integration to the Equation of the Conduction of Heat. Proc. Edin. Math. Soc. Vol. XIX. 1901.
page 46 note * Bryan. An Applieation of the Method of Images to the Conduction of Heat. Proo. Lond. Math. Soc. Vol. XXII. 1891.
page 46 note † A Problem in Conduction of Heat. Phil. Mag. July 1902.
page 52 note * Fourier's Heat. Chapter V., Section I.
Kirchhoff. Vorksungen iiber Mathematische Physik, Bd. IV., pp. 30-33.
page 52 note † Knake. Über die Wärme-bewegung in einem von zwei parallelen Wänden begrenzten Korper dessen Begrenzungen mit einem Gose in Berührung stehen.
Diss. Halle. 1871.
Fudzisawa. Über eine in der Wärme-Leitungs-Theorie auftretende, nachden Wurzeln einer transcendentan Gleichung fortschreitende, unendliche Rcihe.
Diss. Strassburg. 1886.
loc. cit. p. 427.
page 55 note * Hankel. Die Cylinder-Functionen erater und zweiter Art.
Math. Ann. Bd. VI., p. 494 (3) and (4).
page 55 note † loc. cit. pp. 496-7.
page 56 note * Reference might also be made to the discussion in Graf and Gubler's Einleitung in die Theorie der Bessel'schen Functionen Enter Heft.
Cf. pp. 34, 35, 82-86. Bern, 1898.
page 56 note † Cf. Gray and Mathew's Treatise, p. 77 (158).
page 57 note * Cf. Sommerfeld. Die Willkurlichen Functionen in der Mathematitchen Physik, §§ 7, 12.
Diss. Königsberg, 1891.
page 58 note * Cf. The approximate value given below for the Bessel's Functions.
page 60 note * Cf. Weber. Über die stationären Strömungen der Electricität in Cylindern.
Crelles' Journal. Bd. 76, p. 10.
Graf u. Gubler, loc. cit. Erstes Heft, pp. 43-45.
page 61 note * Cf. Gray and Mathews. Chapter VI.
page 62 note * Cf. Heine. Einige Anwendungen der Besiduen-Rechnung.
Crelle's Journal, Bd. 89.
page 64 note * Cf. Gray and Mathews, Chapter VI.
page 64 note * Proc. Lond. Math. Soc, Vol. XXX., pp. 151-161.


