Article contents
Unitary bordism of circle actions
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The purpose of this paper is to describe 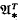 , the bordism module of unitary T-manifolds, where T denotes the circle group S1. We give both an algebraic and a geometric description. The algebraic result is
, the bordism module of unitary T-manifolds, where T denotes the circle group S1. We give both an algebraic and a geometric description. The algebraic result is
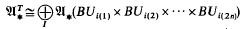
where I = (i(1), i(2),…i(2n)) runs through all finite ordered 2n-tuples (n≧0) of non-negative integers which satisfy the conditions (a) i(l) + i(2n)≠0 and (b) if i(2n)≠0 then i(2n)=≠. The isomorphism is also described geometrically and this leads to geometric generators of 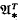 .
.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 26 , Issue 1 , February 1983 , pp. 97 - 105
- Copyright
- Copyright © Edinburgh Mathematical Society 1983
References
REFERENCES
1.Hattori, A. and Taniguchi, H., Smooth S 1-action and bordism, J. Math. Soc. Japan 24 (1972), 701–731.CrossRefGoogle Scholar
2.Kosniowski, C., Applications of the holomorphic Lefschetz formula, Bull. Lond. Math. Soc. 2 (1970), 43–48.CrossRefGoogle Scholar
3.Kosniowski, C., Actions of finite abelian groups (Pitman, London-San Francisco-Melbourne,1978).Google Scholar
- 8
- Cited by


