Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T21:19:53.820Z Has data issue: false hasContentIssue false
  • English
  • Français

Twisted Alexander ideals and the isomorphism problem for a family of parafree groups

Part of: Low-dimensional topology

Published online by Cambridge University Press:  22 June 2020

Do Viet Hung  and
Vu The Khoi
Do Viet Hung
Affiliation:
Ha Giang College of Education, Ha Giang, Vietnam ([email protected])
Vu The Khoi
Affiliation:
Institute of Mathematics, VietNam Academy of Science and Technology, 18 Hoang Quoc Viet, Hanoi10307, Vietnam ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1969, Baumslag introduced a family of parafree groups Gi,j which share many properties with the free group of rank 2. The isomorphism problem for the family Gi,j is known to be difficult; a few small partial results have been found so far. In this paper, we compute the twisted Alexander ideals of the groups Gi,j associated with non-abelian representations into 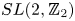$SL(2,{\mathbb Z}_2)$. Using the twisted Alexander ideals, we prove that several pairs of groups among Gi,j are not isomorphic. As a consequence, we solve the isomorphism problem for sub-families containing infinitely many groups Gi,j.

Keywords

group isomorphism problemtwisted Alexander idealparafree groups

MSC classification

Secondary: 57M05: Fundamental group, presentations, free differential calculus
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 3 , August 2020 , pp. 780 - 806
Check for updates
Copyright
Copyright © The Authors, 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alexander, J. W., Topological invariants of knots and links, Trans. Am. Math. Soc. 30 (1928), 275–306.10.1090/S0002-9947-1928-1501429-1CrossRefGoogle Scholar
2.Baumslag, G., Some groups that are just about free, Bull. Am. Math. Soc. 73 (1967), 621–622.10.1090/S0002-9904-1967-11800-7CrossRefGoogle Scholar
3.Baumslag, G., Groups with the same lower central sequence as a relatively free group II: Properties, Trans. Am. Math. Soc. 142 (1969), 507–538.10.1090/S0002-9947-1969-0245653-3CrossRefGoogle Scholar
4.Baumslag, G. and Cleary, S., Parafree one-relator groups, J. Group Theory 9(2) (2006), 191–201.10.1515/JGT.2006.013CrossRefGoogle Scholar
5.Baumslag, G., Cleary, S. and Havas, G., Experimenting with infinite groups, I, Exp. Math. 13(4) (2004), 495–502.10.1080/10586458.2004.10504558CrossRefGoogle Scholar
6.Chandler, B. and Magnus, W., The history of combinatorial group theory, Studies in the History of Mathematics and Physical Sciences, Volume 9 (Springer, New York, 1982).10.1007/978-1-4613-9487-7CrossRefGoogle Scholar
7.Fine, B., Rosenberger, G. and Stille, M., The isomorphism problem for a class of para-free groups, Proc. Edinb. Math. Soc. 40(3) (1997), 541–549.10.1017/S0013091500024007CrossRefGoogle Scholar
8.Fox, R. H., Free differential calculus, I: Derivation in the free group ring, Ann. of Math. 57 (1953), 547–560.10.2307/1969736CrossRefGoogle Scholar
9.Fox, R. H., Free differential calculus, II: The isomorphism problem of groups, Ann. of Math. 59 (1954), 196–210.10.2307/1969686CrossRefGoogle Scholar
10.Hironaka, E., Alexander stratifications of character varieties, Ann. Inst. Fourier 47(2) (1997), 555–583.10.5802/aif.1573CrossRefGoogle Scholar
11.Hung, D. V. and Khoi, V. T., Applications of the Alexander ideals to the isomorphism problem for families of groups, Proc. Edinb. Math. Soc. 60(1) (2017), 177–185.10.1017/S001309151600002XCrossRefGoogle Scholar
12.Ishii, A., Nikkuni, R. and Oshiro, K., On calculations of the twisted Alexander ideals for spatial graphs, handlebody-knots and surface-links, Osaka J. Math. 55(2) (2018), 297–313.Google Scholar
13.Lewis, R. H. and Liriano, S., Isomorphism classes and derived series of certain almost-free groups, Exp. Math. 3(3) (1994), 255–258.10.1080/10586458.1994.10504294CrossRefGoogle Scholar
14.Lin, X. S., Representations of knot groups and twisted Alexander polynomials, Acta Math. Sin. 17(3) (2001), 361–380.10.1007/s101140100122CrossRefGoogle Scholar
15.Wada, M., Twisted Alexander polynomial for finitely presentable group, Topology 33 (1994), 241–256.10.1016/0040-9383(94)90013-2CrossRefGoogle Scholar