Article contents
Total mean curvature surfaces in the product space  ${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
Published online by Cambridge University Press: 26 April 2023
Abstract
The total mean curvature functional for submanifolds into the Riemannian product space  $\mathbb{S}^n\times\mathbb{R}$ is considered and its first variational formula is presented. Later on, two second-order differential operators are defined and a nice integral inequality relating both of them is proved. Finally, we prove our main result: an integral inequality for closed stationary
$\mathbb{S}^n\times\mathbb{R}$ is considered and its first variational formula is presented. Later on, two second-order differential operators are defined and a nice integral inequality relating both of them is proved. Finally, we prove our main result: an integral inequality for closed stationary 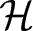 $\mathcal{H}$-surfaces in
$\mathcal{H}$-surfaces in  $\mathbb{S}^n\times\mathbb{R}$, characterizing the cases where the equality is attained.
$\mathbb{S}^n\times\mathbb{R}$, characterizing the cases where the equality is attained.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
- 1
- Cited by



