Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T20:57:14.277Z Has data issue: false hasContentIssue false
  • English
  • Français

Toeplitz operators with distributional symbols on Bergman spaces

Part of: Special classes of linear operators

Published online by Cambridge University Press:  07 April 2011

Antti Perälä ,
Jari Taskinen  and
Jani Virtanen
Antti Perälä
Affiliation:
Department of Mathematics, University of Helsinki, 00014 Helsinki, Finland ([email protected]; [email protected])
Jari Taskinen
Affiliation:
Department of Mathematics, University of Helsinki, 00014 Helsinki, Finland ([email protected]; [email protected])
Jani Virtanen
Affiliation:
Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, NY 10012, USA ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the boundedness and compactness of Toeplitz operators Ta on Bergman spaces 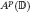, 1 < p < ∞. The novelty is that we allow distributional symbols. It turns out that the belonging of the symbol to a weighted Sobolev space 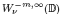of negative order is sufficient for the boundedness of Ta. We show the natural relation of the hyperbolic geometry of the disc and the order of the distribution. A corresponding sufficient condition for the compactness is also derived.

Keywords

Toeplitz operatorBergman spacedistributionbounded operatorcompact operator

MSC classification

Secondary: 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 54 , Issue 2 , June 2011 , pp. 505 - 514
Copyright
Copyright © Edinburgh Mathematical Society 2011

References

1.Adams, R. A., Sobolev spaces (Academic Press, 1975).Google Scholar
2.Alexandrov, A. and Rozenblum, G., Finite rank Toeplitz operators: some extensions of D. Luecking's theorem, J. Funct. Analysis 256 (2009), 2291–2303.Google Scholar
3.Axler, S. and Zheng, D., Compact operators via the Berezin transform, Indiana Univ. Math. J. 47 (1998), 387–400.CrossRefGoogle Scholar
4.Horvath, J., Topological vector spaces and distributions, Volume I (Addison–Wesley, Reading, MA, 1966).Google Scholar
5.Karapetyants, A., The space , compact Toeplitz operators with symbols on weighted Bergman spaces, and the Berezin transform, Izv. VUZ Mat. 8 (2006), 76–79.Google Scholar
6.Rudin, W., Functional analysis (McGraw-Hill, 1973).Google Scholar
7.Suarez, D., The essential norm of operators in the Toeplitz algebra on , Indiana Univ. Math. J. 56 (2007), 2185–2232.Google Scholar
8.Taskinen, J. and Virtanen, J. A., Spectral theory of Toeplitz and Hankel operators on the Bergman space A 1, New York J. Math. 14 (2008), 305–323.Google Scholar
9.Taskinen, J. and Virtanen, J. A., Toeplitz operators on Bergman spaces with locally integrable symbols, Rev. Mat. Ibero. 26(2) (2010), 693–706.Google Scholar
10.Vasilevski, N., Commutative algebras of Toeplitz operators on the Bergman space, Operator Theory: Advances and Applications, Volume 185 (Birkhäuser, 2008).Google Scholar
11.Zhu, K., Positive Toeplitz operators on weighted Bergman spaces of bounded symmetric domains, J. Operat. Theory 20 (1988), 329–357.Google Scholar
12.Zhu, K., BMO and Hankel operators on Bergman spaces, Pac. J. Math. 155 (1992), 377–395.CrossRefGoogle Scholar
13.Zhu, K., Operator theory in function spaces, 2nd edn, Mathematical Surveys and Monographs 138 (American Mathematical Society, Providence, RI, 2007).Google Scholar
14.Zorboska, N., Toeplitz operators with BMO symbols and the Berezin transform, Int. J. Math. Math. Sci. 46 (2003), 2929–2945.CrossRefGoogle Scholar