Article contents
Tilting pairs in extriangulated categories
Published online by Cambridge University Press: 26 October 2021
Abstract
Extriangulated categories were introduced by Nakaoka and Palu to give a unification of properties in exact categories and extension-closed subcategories of triangulated categories. A notion of tilting pairs in an extriangulated category is introduced in this paper. We give a Bazzoni characterization of tilting pairs in this setting. We also obtain the Auslander–Reiten correspondence of tilting pairs which classifies finite $\mathcal {C}$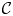 -tilting subcategories for a certain self-orthogonal subcategory $\mathcal {C}$
-tilting subcategories for a certain self-orthogonal subcategory $\mathcal {C}$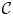 with some assumptions. This generalizes the known results given by Wei and Xi for the categories of finitely generated modules over Artin algebras, thereby providing new insights in exact and triangulated categories.
with some assumptions. This generalizes the known results given by Wei and Xi for the categories of finitely generated modules over Artin algebras, thereby providing new insights in exact and triangulated categories.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 947 - 981
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
- 3
- Cited by



