Tensor products of separable reduced primary modules

Extract

R will denote a Dedekind domain and Pone of its prime ideals. A P-primary module will be an R-module all of whose non-zero elements have annihilators that are powers of the prime P. In all that follows E is such a module.

The height of 0 ≠ x ∈ E will be max{n : x ∈ PⁿE}. It is denoted by h(x). If this maximum does not exist we will say h(x)∞.

Clearly the condition 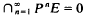is equivalent to E having no non-zero elements of infinite height. Adopting the terminology of (2, Ch. XI) where such modules over the ring of integers are studied, we will call these modules separable and reduced.