Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-23T18:50:44.643Z Has data issue: false hasContentIssue false
  • English
  • Français

A summability method due to linear differential equations and a uniqueness property of solutions of singular differential equations

Published online by Cambridge University Press:  20 January 2009

H. Gingold
H. Gingold
Affiliation:
Technion Institute, Haifa, Israel
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to expose a method which will match a function f(z) existing in a domain D to a formal series 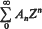whose radius of convergence may be zero. This matching process has to be done in a “natural way”, and has to be “regular”, which means that if a power series 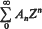converges absolutely in the circle E = {z | |z|<r} then the summability function f(z) produced by our method in the domain D and matched to 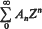will coincide with 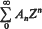in the domain E∩D. Euler, in his time, matched the function 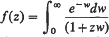to the power series .

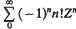Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 20 , Issue 1 , March 1976 , pp. 41 - 51
Copyright
Copyright © Edinburgh Mathematical Society 1976

References

REFERENCES

(1) Hardy, G. H., Divergent series (Clarendon Press, Oxford, 1949).Google Scholar
(2) Cartan, H., Elementary theory of analytic functions of one or several complex variables (Hermann, Paris, 1963).Google Scholar
(3) Wasow, W., Asymptotic expansions for ordinary differential equations (John Wiley & Sons, Inc., New York, London, Sydney, 1965).Google Scholar