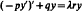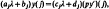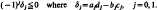Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Binding, Paul
1995.
A New Angle on Sturm-Liouville Problems.
Rocky Mountain Journal of Mathematics,
Vol. 25,
Issue. 1,
Binding, P. A.
and
Browne, Patrick J.
1995.
Application of two parameter eigencurves to Sturm–Liouville problems with eigenparameter-dependent boundary conditions.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 125,
Issue. 6,
p.
1205.
Browne, Patrick J
and
Sleeman, B D
1996.
Inverse nodal problems for Sturm - Liouville equations with eigenparameter dependent boundary conditions.
Inverse Problems,
Vol. 12,
Issue. 4,
p.
377.
Browne, Patrick J
and
Sleeman, B D
1997.
A uniqueness theorem for inverse eigenparameter dependent Sturm - Liouville problems.
Inverse Problems,
Vol. 13,
Issue. 6,
p.
1453.
Binding, P. A.
and
Browne, Patrick J.
1997.
Oscillation theory for indefinite Sturm-Liouville problems with eigenparameter-dependent boundary conditions.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 127,
Issue. 6,
p.
1123.
Browne, Patrick J.
1998.
A Prüfer approach to half-linear Sturm-Liouville problems.
Proceedings of the Edinburgh Mathematical Society,
Vol. 41,
Issue. 3,
p.
573.
Kerimov, N. B.
and
Mamedov, Kh. R.
1999.
On one boundary value problem with a spectral parameter in the boundary conditions.
Siberian Mathematical Journal,
Vol. 40,
Issue. 2,
p.
281.
Бен Амара, Жамель
Ben Amara, Jamel
Шкаликов, Андрей Андреевич
and
Shkalikov, Andrei Andreevich
1999.
Задача Штурма - Лиувилля с физическим и спектральным параметрами в граничном условии.
Математические заметки,
Vol. 66,
Issue. 2,
p.
163.
Binding, Paul A.
Browne, Patrick J.
and
Watson, Bruce A.
2000.
Spectral Problems for Non-Linear Sturm-Liouville Equations with Eigenparameter Dependent Boundary Conditions.
Canadian Journal of Mathematics,
Vol. 52,
Issue. 2,
p.
248.
Bhattacharyya, T
Binding, P.A
and
Seddighi, K
2001.
Multiparameter Sturm–Liouville Problems with Eigenparameter Dependent Boundary Conditions.
Journal of Mathematical Analysis and Applications,
Vol. 264,
Issue. 2,
p.
560.
Binding, Paul A.
Browne, Patrick J.
and
Watson, Bruce A.
2002.
Sturm–Liouville problems with boundary conditions rationally dependent on the eigenparameter, II.
Journal of Computational and Applied Mathematics,
Vol. 148,
Issue. 1,
p.
147.
Binding, Paul A.
Browne, Patrick J.
and
Watson, Bruce A.
2002.
Linear Operators and Matrices.
p.
135.
Binding, Paul
Browne, Patrick
and
Watson, Bruce
2002.
Spectral asymptotics for Sturm-Liouville equations with indefinite weight.
Transactions of the American Mathematical Society,
Vol. 354,
Issue. 10,
p.
4043.
2003.
Non-Self-Adjoint Boundary Eigenvalue Problems.
Vol. 192,
Issue. ,
p.
475.
Maeve McCarthy, C.
and
Rundell, William
2003.
Eigenparameter Dependent Inverse Sturm-Liouville Problems.
Numerical Functional Analysis and Optimization,
Vol. 24,
Issue. 1-2,
p.
85.
Binding, Paul
2003.
A hierarchy of Sturm–Liouville problems.
Mathematical Methods in the Applied Sciences,
Vol. 26,
Issue. 4,
p.
349.
Binding, Paul A.
Browne, Patrick J.
and
Watson, Bruce A.
2004.
Equivalence of inverse Sturm–Liouville problems with boundary conditions rationally dependent on the eigenparameter.
Journal of Mathematical Analysis and Applications,
Vol. 291,
Issue. 1,
p.
246.
Бен Амара, Жамель
Ben Amara, Jamel
Владимиров, Антон Алексеевич
and
Vladimirov, Anton Alekseevich
2004.
Об одной задаче четвертого порядка со спектральным и физическим параметрами в граничном условии.
Известия Российской академии наук. Серия математическая,
Vol. 68,
Issue. 4,
p.
3.
Amara, Jamel Ben
2004.
Functional Analysis and its Applications - Proceedings of the International Conference on Functional Analysis and its Applications Dedicated to the 110th Anniversary of Stefan Banach, May 28-31, 2002, Lviv, Ukraine.
Vol. 197,
Issue. ,
p.
49.
Binding, Paul A.
Browne, Patrick J.
and
Watson, Bruce A.
2004.
Recovery of the m-function from spectral data for generalized Sturm–Liouville problems.
Journal of Computational and Applied Mathematics,
Vol. 171,
Issue. 1-2,
p.
73.