Article contents
Stable solutions to double phase problems involving a nonlocal term
Published online by Cambridge University Press: 23 October 2023
Abstract
In this paper, we study weak solutions, possibly unbounded and sign-changing, to the double phase problem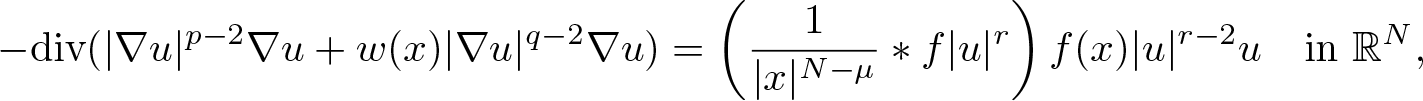 \begin{equation*}-\text{div} (|\nabla u|^{p-2} \nabla u + w(x)|\nabla u|^{q-2} \nabla u) = \left(\frac{1}{|x|^{N-\mu}}*f|u|^r\right) f(x)|u|^{r-2}u \quad\text{in}\ \mathbb{R}^N,\end{equation*}
\begin{equation*}-\text{div} (|\nabla u|^{p-2} \nabla u + w(x)|\nabla u|^{q-2} \nabla u) = \left(\frac{1}{|x|^{N-\mu}}*f|u|^r\right) f(x)|u|^{r-2}u \quad\text{in}\ \mathbb{R}^N,\end{equation*} $q\ge p\ge2$, r > q,
$q\ge p\ge2$, r > q, 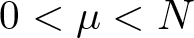 $0 \lt \mu \lt N$ and
$0 \lt \mu \lt N$ and 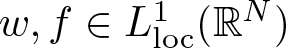 $w,f \in L^1_{\rm loc}(\mathbb{R}^N)$ are two non-negative functions such that
$w,f \in L^1_{\rm loc}(\mathbb{R}^N)$ are two non-negative functions such that 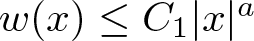 $w(x) \le C_1|x|^a$ and
$w(x) \le C_1|x|^a$ and 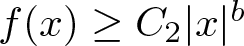 $f(x) \ge C_2|x|^b$ for all
$f(x) \ge C_2|x|^b$ for all 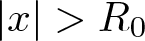 $|x| \gt R_0$, where
$|x| \gt R_0$, where 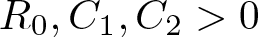 $R_0,C_1,C_2 \gt 0$ and
$R_0,C_1,C_2 \gt 0$ and 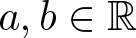 $a,b\in\mathbb{R}$. Under some appropriate assumptions on p, q, r, µ, a, b and N, we prove various Liouville-type theorems for weak solutions which are stable or stable outside a compact set of
$a,b\in\mathbb{R}$. Under some appropriate assumptions on p, q, r, µ, a, b and N, we prove various Liouville-type theorems for weak solutions which are stable or stable outside a compact set of 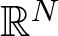 $\mathbb{R}^N$. First, we establish the standard integral estimates via stability property to derive the non-existence results for stable weak solutions. Then, by means of the Pohožaev identity, we deduce the Liouville-type theorem for weak solutions which are stable outside a compact set.
$\mathbb{R}^N$. First, we establish the standard integral estimates via stability property to derive the non-existence results for stable weak solutions. Then, by means of the Pohožaev identity, we deduce the Liouville-type theorem for weak solutions which are stable outside a compact set.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 4 , November 2023 , pp. 1119 - 1141
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
Footnotes
The online version of this article has been updated since original publication. A notice detailing the changes has also been published at DOI https://doi.org/10.1017/S0013091523000718
References
A correction has been issued for this article:
- 2
- Cited by
Linked content
Please note a has been issued for this article.



