Spectral Multipliers for Laplacians Associated with some Dirichlet Forms

Abstract

Let 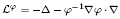be the self-adjoint operator associated with the Dirichlet form

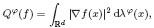
where ϕ is a positive C² function, dλ^ϕ = ϕdλ and λ denotes Lebesgue measure on ℝ^d. We study the boundedness on L^p(λ^ϕ) of spectral multipliers of 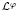. We prove that if ϕ grows or decays at most exponentially at infinity and satisfies a suitable ‘curvature condition’, then functions which are bounded and holomorphic in the intersection of a parabolic region and a sector and satisfy Mihlin-type conditions at infinity are spectral multipliers of L^p(λ^ϕ). The parabolic region depends on ϕ, on p and on the infimum of the essential spectrum of the operator 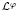on L²(λ^ϕ). The sector depends on the angle of holomorphy of the semigroup generated by 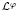on L^p(λ^ϕ).