Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-04T19:04:35.307Z Has data issue: false hasContentIssue false
  • English
  • Français

A spectral mapping theorem for some representations of compact abelian groups

Published online by Cambridge University Press:  20 January 2009

Sin-Ei Takahasi  and
Jyunji Inoue
Sin-Ei Takahasi
Affiliation:
Department of Basic TechnologyApplied Mathematics and PhysicsYamagata UniversityYonezawa 992, Japan
Jyunji Inoue
Affiliation:
Department of MathematicsHokkaido UniversitySapporo 060, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if G is a compact abelian group and U is a weakly continuous representation of G by means of isometries on a Banach space X, then 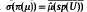holds for each measure µ in reg(M(G)), where π(µ) denotes the generalized convolution operator in B(X) defined by 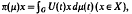, σ the usual spectrum in B(X), sp(U) the Arveson spectrum of U, 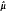the Fourier-Stieltjes transform of µ and reg(M(G)) the largest closed regular subalgebra of the convolution measure algebra M(G) of G. reg(M(G)) contains all the absolutely continuous measures and discrete measures.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 35 , Issue 1 , February 1992 , pp. 47 - 52
Copyright
Copyright © Edinburgh Mathematical Society 1992

References

REFERENCES

1.Albrecht, E., Decomposable systems of operators in harmonic analysis, in Toeplitz Centennial (Goldberg, I. (ed.), Birkhauser, Basel, 1982), 19–35.CrossRefGoogle Scholar
2.D'Antoni, C., Longo, R. and Zsido, L., A spectral mapping theorem for locally compact groups of operators, Pacific J. Math. 103 (1981), 17–24.CrossRefGoogle Scholar
3.Arveson, W., On groups of automorphisms of operator algebras, J. Funct. Anal. 15 (1974), 217–243.CrossRefGoogle Scholar
4.Connes, A., Une classification des facteurs de type III, Ann. Sci. Ecole Norm. Sup. 6 (1973), 133.CrossRefGoogle Scholar
5.Eschmeier, J., Operator decomposability and weakly continuous representations of locally compact abelian groups, J. Operator Theory 7 (1982), 201–208.Google Scholar
6.Inoue, J., Some closed subalgebras of measure algebras and a generalization of P. J. Cohen's theorem, J. Math. Soc. Japan 23 (1971), 278–294.CrossRefGoogle Scholar
7.Inoue, J. and Takahasi, S.-E., A remark on the largest regular subalgebra of a Banach algebra, Proc. Amer. Math. Soc., to appear.Google Scholar
8.Larsen, R., An introduction to the theory of multipliers (Springer-Verlag, New York-Heidelberg, 1971).CrossRefGoogle Scholar
9.Larsen, R., Banach Algebras (Marcel Dekker, Inc., New York, 1973).Google Scholar
10.Takahasi, S.-E. and Hatori, O., Commutative Banach algebras which satisfy Bochner-Schoenberg-Eberlein type theorem, Proc. Amer. Math. Soc. 110 (1990), 149–158.Google Scholar
11.Rickart, C. E., General Theory of Banach Algebras (D. Van Nostrand, Princeton, N.J., 1960).Google Scholar
12.Rickert, N. W., Locally compact topologies for groups, Trans. Amer. Math. Soc. 119 (1965), 150–166.Google Scholar