Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yakubovich, Dmitry
2009.
Vector Semi-Fredholm Toeplitz Operators and Mean Winding Numbers.
Nagoya Mathematical Journal,
Vol. 195,
Issue. ,
p.
57.


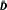 are given. In particular if φ is a unimodular function in
are given. In particular if φ is a unimodular function in 