Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-22T02:12:08.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Some cyclic inequalities

Published online by Cambridge University Press:  20 January 2009

V. J. Baston
V. J. Baston
Affiliation:
The University, Southampton S09 5NH
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we prove some cyclic inequalities which are generalisations of known results. We shall assume throughout that ai+n = ai ≧ 0 for all i, that no denominator in the statement of a result vanishes and finally that p, m and q are positive integers. We shall also use A(i, m) to denote 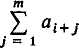with the convention that A(i, 0) = 0. The most interesting of our results is probably Theorem 2 since, in the special case p = 1, m = 2, r = 0, it gives a lower bound of ⅓n for the Shapiro sum 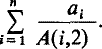. Although it is by no means best possible, see (2), our method implicitly gives a really simple way of obtaining this lower bound which, incidentally, is an improvement on Rankin's original result (5).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 2 , September 1974 , pp. 115 - 118
Copyright
Copyright © Edinburgh Mathematical Society 1974

References

REFERENCES

(1) Boarder, J. C. and Daykin, D. E., Inequalities for certain cyclic sums II, Proc. Edinburgh Math. Soc. 18 (1973), 209–218.CrossRefGoogle Scholar
(2) Diananda, P. H., A cyclic inequality and an extension of it II, Proc. Edinburgh Math. Soc. 13 (1962), 143–152.CrossRefGoogle Scholar
(3) Diananda, P. H., Some cyclic and other inequalities, Proc. Cambridge Philos. Soc. 58 (1962), 425–427.CrossRefGoogle Scholar
(4) Daykin, D. E., Inequalities for functions of a cyclic nature, J. London Math. Soc. 3 (1971), 453–462.CrossRefGoogle Scholar
(5) Rankin, R. A., A cyclic inequality, Proc. Edinburgh Math. Soc. 12 (1961), 139–147.CrossRefGoogle Scholar
(6) Zulauf, A., Note on some inequalities, Math. Gaz. 43 (1959), 42–44.Google Scholar