Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-29T01:02:18.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Some analytical properties of the matrix related to q-coloured Delannoy numbers

Part of: Limit theorems Polynomials, rational functions Combinatorics Special matrices

Published online by Cambridge University Press:  06 October 2022

Lili Mu  and
Sai-Nan Zheng
Lili Mu
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, PR China ([email protected])
Sai-Nan Zheng
Affiliation:
School of Data Science and Artificial Intelligence, Dongbei University of Finance and Economics, Dalian 116025, PR China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The $q$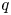-coloured Delannoy numbers $D_{n,k}(q)$ 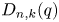count the number of lattice paths from $(0,\,0)$ 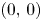to $(n,\,k)$ 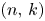using steps $(0,\,1)$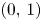, $(1,\,0)$ 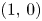and $(1,\,1)$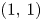, among which the $(1,\,1)$ 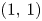steps are coloured with $q$ 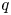colours. The focus of this paper is to study some analytical properties of the polynomial matrix $D(q)=[d_{n,k}(q)]_{n,k\geq 0}=[D_{n-k,k}(q)]_{n,k\geq 0}$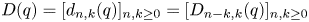, such as the strong $q$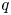-log-concavity of polynomial sequences located in a ray or a transversal line of $D(q)$ 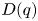and the $q$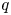-total positivity of $D(q)$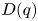. We show that the zeros of all row sums $R_n(q)=\sum \nolimits _{k=0}^{n}d_{n,k}(q)$ 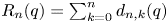are in $(-\infty,\, -1)$ 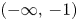and are dense in the corresponding semi-closed interval. We also prove that the zeros of all antidiagonal sums $A_n(q)=\sum \nolimits _{k=0}^{\lfloor n/2 \rfloor }d_{n-k,k}(q)$ 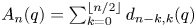are in the interval $(-\infty,\, -1]$ 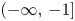and are dense there.

Keywords

strong q-log-concavityq-total positivitypolynomial matrixDelannoy trianglepolynomial with only real zeros

MSC classification

Primary: 05A20: Combinatorial inequalities 15B99: None of the above, but in this section 26C10: Polynomials 60F05: Central limit and other weak theorems
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 3 , August 2022 , pp. 847 - 860
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banderier, C. and Schwer, S., Why Delannoy numbers?, J. Statist. Plann. Inference 135 (2005), 40–54.CrossRefGoogle Scholar
Barry, P., On integer-sequence-based constructions of generalized Pascal triangles, J. Integer Seq. 9 (2006), 06.2.4.Google Scholar
Bender, E. A., Central and local limit theorems applied to asymptotic enumeration, J. Combin. Theory Ser. A 15 (1973), 91–111.CrossRefGoogle Scholar
Beraha, S., Kahane, J. and Weiss, N., Limits of zeros of recursively defined families of polynomials, in Studies in Foundations and Combinatorics (ed. G. Rota), pp. 213–232, Advances in Mathematics, Supplementary Studies, Volume 1 (Academic Press, New York, 1978).Google Scholar
Butler, L. M., The $q$-log concavity of $q$-binomial coefficients, J. Combin. Theory Ser. A 54 (1990), 54–63.CrossRefGoogle Scholar
Canfield, E. R., Asymptotic normality in enumeration, Handbook of enumerative combinatorics, pp. 255–280, Discrete Math. Appl. (Boca Raton) (CRC Press, Boca Raton, FL, 2015).Google Scholar
Gutman, I. and Borovićanin, B., Zhang-Zhang polynomial of multiple linear hexagonal chains, Z. Naturforsch. 61a (2006), 73–77.CrossRefGoogle Scholar
Leroux, P., Reduced matrices and $q$-log concavity of $q$-Stirling numbers, J. Combin. Theory Ser. A 54 (1990), 64–84.CrossRefGoogle Scholar
Liu, L. L. and Wang, Y., On the log-convexity of combinatorial sequences, Adv. Appl. Math. 39 (2007), 453–476.CrossRefGoogle Scholar
Maló, E., Note sur les équations algébriques dont toutes les racines sont réeles, J. Math. Spéc. 4 (1895), 7–10.Google Scholar
Mao, J., Mu, L. and Wang, Y., Yet another criterion for the total positivity of Riordan arrays, Linear Algebra Appl. 634 (2022), 106–111.CrossRefGoogle Scholar
Mu, L. and Zheng, S.-N., On the total positivity of Delannoy-like triangles, J. Integer Seq. 20 (2017), 17.1.6.Google Scholar
Sagan, B. E., Log concave sequences of symmetric functions and analogs of the Jacobi-Trudi determinants, Trans. Amer. Math. Soc. 329 (1992), 795–811.CrossRefGoogle Scholar
Sloane, N., The on-line encyclopedia of integer sequences, http://oeis.orgGoogle Scholar
Su, X.-T. and Wang, Y., On unimodality problems in Pascal's triangle, Electron. J. Combin. 15 (2008), #R113.CrossRefGoogle Scholar
Sulanke, R. A., Objects counted by the central Delannoy numbers, J. Integer Seq. 6 (2003), 03.1.5.Google Scholar
Sun, Z., On Delannoy numbers and Schröder numbers, J. Number Theory 131 (2011), 2387–2397.CrossRefGoogle Scholar
Sun, Z., Arithmetic properties of Delannoy numbers and Schröder numbers, J. Number Theory 183 (2018), 146–171.CrossRefGoogle Scholar
Torres, A., Cabada, A. and Nieto, J., An exact formula for the number of alignments between two DNA sequences, DNA Sequence 14 (2003), 227–430.CrossRefGoogle ScholarPubMed
Tran, K. and Zumba, A., Zeros of polynomials with four-term recurrence, Involve 11 (2018), 501–518.CrossRefGoogle Scholar
Wang, Y., Zheng, S.-N. and Chen, X., Analytic aspects of Delannoy numbers, Discrete Math. 342 (2019), 2270–2277.CrossRefGoogle Scholar
Wang, Y., Zhang, H.-X. and Zhu, B.-X., Asymptotic normality of Laplacian coefficients of graphs, J. Math. Anal. Appl. 455 (2017), 2030–2037.CrossRefGoogle Scholar
Wang, Y. and Zhu, B. X., Log-convex and Stieltjes moment sequences, Adv. Appl. Math. 81 (2016), 115–127.CrossRefGoogle Scholar
Yu, Y., Confirming two conjectures of Su and Wang on binomial coefficients, Adv. Appl. Math. 43 (2009), 317–322.CrossRefGoogle Scholar
Yang, S.-L., Zheng, S.-N., Yuan, S.-P. and He, T.-X., Schröder matrix as inverse of Delannoy matrix, Linear Algebra Appl. 439 (2013), 3605–3614.CrossRefGoogle Scholar
Zhu, B. X., Log-convexity and strong $q$-log-convexity for some triangular arrays, Adv. Appl. Math. 50 (2013), 595–606.CrossRefGoogle Scholar
Zhu, B. X., q-log-convexity from linear transformations and polynomials with only real zeros, European J. Combin. 73 (2018), 231–246.CrossRefGoogle Scholar