Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T12:26:07.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Soliton solutions for a class of Schrödinger equations with a positive quasilinear term and critical growth

Part of: Equations and inequalities involving nonlinear operators Elliptic equations and systems Equations of mathematical physics and other areas of application Partial differential equations

Published online by Cambridge University Press:  18 February 2022

João Marcos do Ó Open the ORCID record for João Marcos do Ó [Opens in a new window] ,
Elisandra Gloss Open the ORCID record for Elisandra Gloss [Opens in a new window]  and
Uberlandio Severo Open the ORCID record for Uberlandio Severo [Opens in a new window]
João Marcos do Ó
Affiliation:
Departamento de Matemática, Universidade Federal da Paraíba, 58051-900João Pessoa, PB, Brazil ([email protected]; [email protected]; [email protected])
Elisandra Gloss
Affiliation:
Departamento de Matemática, Universidade Federal da Paraíba, 58051-900João Pessoa, PB, Brazil ([email protected]; [email protected]; [email protected])
Uberlandio Severo
Affiliation:
Departamento de Matemática, Universidade Federal da Paraíba, 58051-900João Pessoa, PB, Brazil ([email protected]; [email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the following class of quasilinear Schrödinger equations proposed in plasma physics and nonlinear optics $-\Delta u+V(x)u+\frac {\kappa }{2}[\Delta (u^{2})]u=h(u)$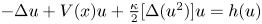 in the whole two-dimensional Euclidean space. We establish the existence and qualitative properties of standing wave solutions for a broader class of nonlinear terms $h(s)$ 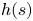with the critical exponential growth. We apply the dual approach to obtain solutions in the usual Sobolev space $H^{1}(\mathbb {R}^{2})$ 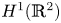when the parameter $\kappa >0$ 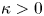is sufficiently small. Minimax techniques, Trudinger–Moser inequality and the Nash–Moser iteration method play an essential role in establishing our results.

Keywords

quasilinear Schrödinger equationstanding wavescritical exponential growthNash–Moser iteration

MSC classification

Primary: 35Q55: NLS-like equations (nonlinear Schrödinger) 35J60: Nonlinear elliptic equations 47J30: Variational methods
Secondary: 35B33: Critical exponents 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 279 - 301
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adimurthi, Existence of positive solutions of the semilinear Dirichlet problem with critical growth for the $n-$Laplacian, Annali della Scuola Normale Superiore di Pisa – Classe di Scienze 17 (1990), 393–413.Google Scholar
Adachi, S., Shibata, M. and Watanabe, T., Asymptotic behavior of positive solutions for a class of quasilinear elliptic equations in $\mathbb {R}^{2}$, Funkcial. Ekvac. 57 (2014), 297–317.CrossRefGoogle Scholar
Aires, J. and Souto, M., Equation with positive coefficient in the quasilinear term and vanishing potential, Topolog. Meth. Nonlin. Anal. 46 (2015), 813–833.Google Scholar
Ambrosetti, A. and Wang, Z.-Q., Positive solutions to a class of quasilinear elliptic equations on $\mathbb {R}$, Discrete Contin. Dyn. Syst. 9 (2003), 55–68.CrossRefGoogle Scholar
Alves, C., Wang, Y. and Shen, Y., Soliton solutions for a class of quasilinear Schrödinger equations with a parameter, J. Differ. Equ. 259 (2015), 318–343.CrossRefGoogle Scholar
Boccardo, L. and Murat, F., Almost everywhere convergence of the gradients of solutions to elliptic and parabolic equations, Nonlinear Anal. 19 (1992), 581–597.CrossRefGoogle Scholar
Cao, D. M., Nontrivial solution of semilinear elliptic equation with critical exponent in $\mathbb {R}^{2}$, Comm. Partial Differ. Equ. 17 (1992), 407–435.CrossRefGoogle Scholar
Colin, M. and Jeanjean, L., Solutions for a quasilinear Schrödinger equation: a dual approach, Nonlinear Anal. 56 (2004), 213–226.CrossRefGoogle Scholar
de Figueiredo, D. G., Miyagaki, O. H. and Ruf, B., Elliptic equations in $\mathbb {R}^{2}$ with nonlinearities in the critical growth range, Calc. Var. Partial Differ. Equ. 3 (1995), 139–153.CrossRefGoogle Scholar
de Souza, M., Severo, U. B. and Vieira, G. F., On a nonhomogeneous and singular quasilinear equation involving critical growth in $\mathbb {R}^{2}$, Comput. Math. Appl. 74 (2017), 513–531.CrossRefGoogle Scholar
de Figueiredo, D. G., do Ó, J. M. and Ruf, B., Elliptic equations and systems with critical Trudinger-Moser nonlinearities, Discrete Contin. Dyn. Syst., 30 (2011), 455–476.CrossRefGoogle Scholar
do Ó, J. M., $N$-Laplacian equations in $\mathbb {R}^{N}$ with critical growth, Abstr. Appl. Anal. 2 (1997), 301–315.CrossRefGoogle Scholar
do Ó, J. M. and Moameni, A., Solitary waves for quasilinear Schrödinger equations arising in plasma physics, Adv. Nonlinear Stud. 9 (2009), 479–497.CrossRefGoogle Scholar
do Ó, J. M. and Severo, U. B., Solitary waves for a class of quasilinear Schrödinger equations in dimension two, Calc. Var. Partial Differ. Equ. 38 (2010), 275–315.CrossRefGoogle Scholar
do Ó, J. M., Miyagaki, O. and Soares, S., Soliton solutions for quasilinear Schrödinger equations: the critical exponential case, Nonlinear Anal. 67 (2007), 3357–3372.CrossRefGoogle Scholar
do Ó, J. M., Medeiros, E. and Severo, U., On the existence of signed and sign-changing solutions for a class of superlinear Schrödinger equations, J. Math. Anal. Appl. 342 (2008), 432–445.CrossRefGoogle Scholar
do Ó, J. M., Miyagaki, O. and Soares, S., Soliton solutions for quasilinear Schrödinger equations with critical growth, J. Differ. Equ. 248 (2010), 722–744.CrossRefGoogle Scholar
Goldman, M. V., Strong turbulence of plasma waves, Rev. Modern Phys. 56 (1984), 709–735.CrossRefGoogle Scholar
Huang, C. and Jia, G., Existence of positive solutions for supercritical quasilinear Schrödinger elliptic equations, J. Math. Anal. Appl. 472 (2019), 705–727.CrossRefGoogle Scholar
Jeanjean, L. and Tanaka, K., A remark on least energy solutions in $\mathbb {R}^{N}$, Proc. Amer. Math. Soc. 131 (2003), 2399–2408.CrossRefGoogle Scholar
Kavian, O., Introduction á la théorie des points critiques et applications aux problèmes elliptiques (Springer-Verlag, Paris, 1993).Google Scholar
Kurihara, S., Large-amplitude quasi-solitons in superfluids films, J. Phys. Soc. Japan 50 (1981), 3262–3267.CrossRefGoogle Scholar
Liu, J. and Wang, Z.-Q., Soliton solutions for quasilinear Schrödinger equations. I, Proc. Amer. Math. Soc. 131 (2003), 441–448.CrossRefGoogle Scholar
Liu, J., Wang, Y. and Wang, Z.-Q., Soliton solutions for quasilinear Schrödinger equations II, J. Differ. Equ. 187 (2003), 473–493.CrossRefGoogle Scholar
Liu, J., Wang, Y. and Wang, Z.-Q., Solutions for Quasilinear Schrödinger Equations via the Nehari Method, Comm. Partial Differ. Equ. 29 (2004), 879–901.CrossRefGoogle Scholar
Liu, X.-Q, Liu, J.-Q and Wang, Z.-Q, Quasilinear elliptic equations via perturbation method, Proc. Amer. Math. Soc. 141 (2013), 253–263.CrossRefGoogle Scholar
Moameni, A., On a class of periodic quasilinear Schrödinger equations involving critical growth in $\mathbb {R}^{2}$, J. Math. Anal. Appl. 334 (2007), 775–786.CrossRefGoogle Scholar
Poppenberg, M., Schmitt, K. and Wang, Z.-Q., On the existence of soliton solutions to quasilinear Schrödinger equations, Calc. Var. Partial Differ. Equ. 14 (2002), 329–344.CrossRefGoogle Scholar
Porkolab, M. and Goldman, M. V., Upper-hybrid solitons and oscillating two-stream instabilities, Phys. Fluids. 19 (1978), 872–881.CrossRefGoogle Scholar
Ruiz, D. and Siciliano, G., Existence of ground states for a modified nonlinear Schrödinger equation, Nonlinearity 23 (2010), 1221–1233.CrossRefGoogle Scholar
Severo, U., Gloss, E. and da Silva, E., On a class of quasilinear Schrödinger equations with superlinear or asymptotically linear terms, J. Differ. Equ. 263 (2017), 3550– 3580.CrossRefGoogle Scholar
Wang, Y., A class of quasilinear Schrödinger equations with critical or supercritical exponents, Comput. Math. Appl. 70 (2015), 562–572.CrossRefGoogle Scholar
Wang, Y., Zhang, Y. and Shen, Y., Multiple solutions for quasilinear Schrödinger equations involving critical exponent, Appl. Math. Comput. 216 (2010), 849–856.Google Scholar
Willem, M., Minimax theorems (Birkhäuser Boston Inc, Boston, 1996).CrossRefGoogle Scholar
Yang, J., Wang, Y. and Abdelgadir, A., Soliton solutions for quasilinear Schrödinger equations, J. Math. Phys. 54 (2013), 071502.CrossRefGoogle Scholar