Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T15:45:12.424Z Has data issue: false hasContentIssue false
  • English
  • Français

Small isomorphisms between operator algebras

Published online by Cambridge University Press:  20 January 2009

Krzysztof Jarosz
Krzysztof Jarosz
Affiliation:
Institute of Mathematics, Warsaw University, Pkin, 00-901 Warsaw, Poland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A and B be function algebras. The well-known Nagasawa theorem [5] states that A and B are isometric if and only if they are isomorphic in the category of Banach algebras. In [2] it was shown that this theorem is stable in the sense that if the Banach–Mazur distance between the underlying Banach spaces of A and B is close to one then these algebras are almost isomorphic, that is there exists a linear map T from A onto B such that 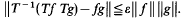. On the other hand one can get from Theorems 1 and 3 of [3] that the Nagasawa theorem can be extended to some operator algebras as follows:

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 2 , June 1985 , pp. 121 - 131
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Jarosz, K., A generalization of the Banach-Stone theorem, Studia Math. 73 (1982), 33–39.CrossRefGoogle Scholar
2.Jarosz, K., Metric and algebraic perturbations of function algebras, Proc. Edinburgh Math. Soc. 26 (1983), 383–391.CrossRefGoogle Scholar
3.Jarosz, K., Isometries between injective tensor products of Banach spaces, Pacific J. Math. to appear.Google Scholar
4.Nagasawa, M., Isomorphisms between commutative Banach algebras with application to rings of analytic functions, Kodai Math. Sent. Rep. 11 (1959), 182–188.Google Scholar