No CrossRef data available.
Article contents
A singular perturbation problem for the Lavrent'ev-Bitsadze equation*
Published online by Cambridge University Press: 20 January 2009
Extract
In this note we consider a singular perturbation problem for the equation
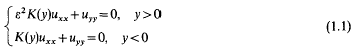
where K(y) = sgn y and. Ε is a small (positive) parameter. This equation for ε≠O is elliptic for y<0 and hyperbolic for y>0. Many of the results carry over to more difficult and interesting problems for equations of mixed type. The particularly simple model treated here permits the elimination of some complications in the analysis involving singular integral equations while preserving the main qualitative features of more general cases. For a special Tricomi-like problem for (1.1) we construct asymptotic expansions in ε, including boundary layer corrections, of the solution. A proof of uniform asymptotic validity of the lowest order terms is given.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 26 , Issue 1 , February 1983 , pp. 49 - 66
- Copyright
- Copyright © Edinburgh Mathematical Society 1983


