Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T20:31:48.299Z Has data issue: false hasContentIssue false
  • English
  • Français

Rings of Polynomials With Artinian Coefficients

Part of: Representation theory of groups Modules, bimodules and ideals Grothendieck groups and $K_0$

Published online by Cambridge University Press:  30 January 2017

F. E. A. Johnson
F. E. A. Johnson*
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the extent to which the weak Euclidean and stably free cancellation properties hold for rings of Laurent polynomials 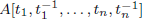with coefficients in an Artinian ring A.

Keywords

stably free cancellationweakly Euclidean ringLaurent polynomials

MSC classification

Secondary: 20C07: Group rings of infinite groups and their modules 16D40: Free, projective, and flat modules and ideals 19A13: Stability for projective modules
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 4 , November 2017 , pp. 947 - 954
Copyright
Copyright © Edinburgh Mathematical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Camps, R. and Dicks, W., On semilocal rings, Israel J. Math. 81 (1993), 203–211.CrossRefGoogle Scholar
2. Cohn, P. M., On the structure of the GL 2 of a ring, Publ. Math. IHES 30 (1966), 5–53.Google Scholar
3. Cohn, P. M., Free rings and their relations (Academic Press, 1985).Google Scholar
4. Dicks, W. and Sontag, E. D., Sylvester domains, J. Pure Appl. Alg. 13 (1978), 243–275.Google Scholar
5. Johnson, F. E. A., Stably free modules over rings of Laurent polynomials, Arch. Math. 97 (2011), 307–317.CrossRefGoogle Scholar
6. Johnson, F. E. A., Syzygies and homotopy theory (Springer, 2011).Google Scholar
7. Lam, T. Y., Serre's problem on projective modules (Springer, 2006).Google Scholar
8. Ojanguran, M. and Sridharan, R., Cancellation of Azumaya algebras, J. Alg. 18 (1971), 501–505.CrossRefGoogle Scholar
9. Reiner, I., Maximal orders (Academic Press, 1975).Google Scholar
10. Smith, H. J. S., On systems of linear indeterminate equations and congruences, Phil. Trans. R. Soc. Lond. 151 (1861), 293–326.Google Scholar
11. Swan, R. G., Strong approximation and locally free modules, in Ring theory and algebra III (ed. McDonald, B.), pp. 153–223 (Marcel Dekker, New York, 1980).Google Scholar
12. Suslin, A. A., On the structure of the special linear group over polynomial rings, Math. USSR Isvestiya 11 (1977), 221–238.Google Scholar
13. Weil, A., Basic number theory (Springer, 1973).CrossRefGoogle Scholar