Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-22T03:53:35.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigid Artinian rings

Published online by Cambridge University Press:  20 January 2009

K. R. McLean
K. R. McLean
Affiliation:
School of EducationUniversity of LiverpoolP.O. Box 147Liverpool L69 3BX
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [4], Maxson studied the properties of a ring R whose only ring endomorphisms φ: R → R are the trivial ones, namely the identity map, idR, and the map 0R given by φ(R) = 0. We shall say that any such ring is rigid, slightly extending the definition used in [4] by dropping the restriction that R2 ≠ 0. Maxson's most detailed results concerned the structure of rigid artinian rings, and our main aim is to complete this part of his investigation by establishing the following

Theorem. Let R(≠0) be a left-artinian ring. Then R is rigid if and only if

(i) 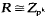, the ring of integers modulo a prime power pk,

(ii) R ≅ N2, the null ring on a cyclic group of order 2, or

(iii) R is a rigid field of characteristic zero.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 25 , Issue 1 , February 1982 , pp. 97 - 99
Copyright
Copyright © Edinburgh Mathematical Society 1982

References

REFERENCES

1.Cohen, I. S., On the structure and ideal theory of complete local rings, Trans. Amer. Math. Soc. 59 (1946), 54–106.CrossRefGoogle Scholar
2.Heerema, N., Derivations on p-adic fields, Trans. Amer. Math. Soc. 102 (1962), 346–351.Google Scholar
3.Heerema, N., Higher derivations and automorphisms of complete local rings, Bull. Amer. Math. Soc. 76 (1970), 1212–1225.CrossRefGoogle Scholar
4.Maxson, C. J., Rigid rings, Proc. Edinburgh Math. Soc. 21 (1978), 95–101.CrossRefGoogle Scholar