Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-04T01:36:22.257Z Has data issue: false hasContentIssue false
  • English
  • Français

Right-angled Artin groups and the cohomology basis graph

Part of: Graph theory Special aspects of infinite or finite groups Basic linear algebra

Published online by Cambridge University Press:  03 February 2025

Ramón Flores ,
Delaram Kahrobaei ,
Thomas Koberda Open the ORCID record for Thomas Koberda [Opens in a new window]  and
Corentin Le Coz
Ramón Flores*
Affiliation:
Department of Geometry and Topology, University of Seville, Seville, Spain
Delaram Kahrobaei
Affiliation:
Departments of Mathematics and Computer Science, Queens College, CUNY, New York, USA Department of Computer Science, University of York, York, UK Department of Computer Science and Engineering, New York University, Tandon School of Engineering, New York, USA The Initiative for the Theoretical Sciences, CUNY Graduate Center, New York, USA
Thomas Koberda
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA, USA
Corentin Le Coz
Affiliation:
Department of Mathematics: Algebra and Geometry (WE01), Universiteit Gent, Ghent, Belgium
*
Corresponding author: Ramon Flores, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Γ be a finite graph and let 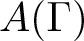$A(\Gamma)$ be the corresponding right-angled Artin group. From an arbitrary basis 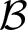$\mathcal B$ of 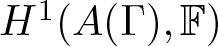$H^1(A(\Gamma),\mathbb F)$ over an arbitrary field, we construct a natural graph 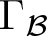$\Gamma_{\mathcal B}$ from the cup product, called the cohomology basis graph. We show that 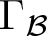$\Gamma_{\mathcal B}$ always contains Γ as a subgraph. This provides an effective way to reconstruct the defining graph Γ from the cohomology of 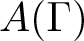$A(\Gamma)$, to characterize the planarity of the defining graph from the algebra of 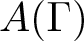$A(\Gamma)$ and to recover many other natural graph-theoretic invariants. We also investigate the behaviour of the cohomology basis graph under passage to elementary subminors and show that it is not well-behaved under edge contraction.

Keywords

determinantcohomologyminorright-angled Artin groupplanar graphouterplanar graph

MSC classification

Primary: 15A15: Determinants, permanents, other special matrix functions
Secondary: 20F36: Braid groups; Artin groups 05C10: Planar graphs; geometric and topological aspects of graph theory 05C83: Graph minors
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 21
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abeles, F. F., Chiò’s and Dodgson’s determinantal identities, Linear Algebra Appl. 454 (2014), 130–137. MR3208413CrossRefGoogle Scholar
Amorós, J., Burger, M., Corlette, K., Kotschick, D. and Toledo, D., Fundamental groups of compact Kähler manifolds, Mathematical Surveys and Monographs, Volume 44 (American Mathematical Society, Providence, RI, 1996). MR1379330CrossRefGoogle Scholar
Brady, N. and Meier, J., Connectivity at infinity for right angled Artin groups, Trans. Amer. Math. Soc. 353(1) (2001), 117–132. MR1675166CrossRefGoogle Scholar
Bridson, M. R. and Reeves, L., On the algorithmic construction of classifying spaces and the isomorphism problem for biautomatic groups, Sci. China Math. 54(8) (2011), 1533–1545. MR2824957CrossRefGoogle Scholar
Brieskorn, E. and Saito, K., Artin-Gruppen und Coxeter-Gruppen, Invent. Math. 17 (1972), 245–271. MR323910CrossRefGoogle Scholar
Brown, K. S., Cohomology of groups, Graduate Texts in Mathematics, Volume 87 (Springer-Verlag, New York, 1994). Corrected reprint of the 1982 original. MR1324339Google Scholar
Charney, R., Artin groups of finite type are biautomatic, Math. Ann. 292(4) (1992), 671–683. MR1157320CrossRefGoogle Scholar
Charney, R., Geodesic automation and growth functions for Artin groups of finite type, Math. Ann. 301(2) (1995), 307–324. MR1314589CrossRefGoogle Scholar
Charney, R., An introduction to right-angled Artin groups, Geom. Dedicata 125 (2007), 141–158. MR2322545CrossRefGoogle Scholar
Chartrand, G., Geller, D. and Hedetniemi, S., Graphs with forbidden subgraphs, J. Combin. Theory Ser. B 10 (1971), 12–41, doi:10.1016/0095-8956(71)90065-7CrossRefGoogle Scholar
de Verdière, Y. C., Sur un nouvel invariant des graphes et un critère de planarité, J. Combin. Theory Ser. B 50(1) (1990), 11–21. MR1070462CrossRefGoogle Scholar
Deligne, P., Les immeubles des groupes de tresses généralisés, Invent. Math. 17 (1972), 273–302. MR422673CrossRefGoogle Scholar
Diestel, R., Graph theory, 5th edition, Graduate Texts in Mathematics, Volume 173 (Springer, Berlin, 2017). MR3644391CrossRefGoogle Scholar
Droms, C., Isomorphisms of graph groups, Proc. Amer. Math. Soc. 100(3) (1987), 407–408. MR891135CrossRefGoogle Scholar
Epstein, D. B. A., Cannon, J. W., Holt, D. F., Levy, S. V. F., Paterson, M. S. and Thurston, W. P., Word processing in groups (Jones and Bartlett Publishers, Boston, MA, 1992). MR1161694CrossRefGoogle Scholar
Flores, R., Kahrobaei, D. and Koberda, T., Algorithmic problems in right-angled Artin groups: complexity and applications, J. Algebra 519 (2019), 111–129. MR3874519CrossRefGoogle Scholar
Flores, R., Kahrobaei, D. and Koberda, T., An algebraic characterization of k-colorability, Proc. Amer. Math. Soc. 149(5) (2021), 2249–2255. MR4232214CrossRefGoogle Scholar
Flores, R., Kahrobaei, D. and Koberda, T., Hamiltonicity via cohomology of right-angled Artin groups, Linear Algebra Appl. 631 (2021), 94–110. MR4308807CrossRefGoogle Scholar
Flores, R., Kahrobaei, D., and Koberda, T., Expanders and right-angled Artin groups, J. Topol. Anal. 16(2) (2024), 155–179, doi:10.1142/S179352532150059X. To appear.CrossRefGoogle Scholar
Gheorghiu, M., Loose ear decompositions and their applications to right-angled artin groups, arXiv:2307.08459, 2023.Google Scholar
Gordon, C., Some embedding theorems and undecidability questions for groups, Combinatorial and geometric group theory (Edinburgh, 1993), London Mathematical Society Lecture Note Series, Volume 204, (Cambridge University Press, Cambridge, 1995). MR1320278Google Scholar
Grossack, C., The right angled artin group functor as a categorical embedding, arXiv:2309.06614, 2024.Google Scholar
Hà, H. and Van Tuyl, A., Monomial ideals, edge ideals of hypergraphs, and their graded Betti numbers, J. Algebraic Combin. 27 (2008), 215–245. MR2375493CrossRefGoogle Scholar
Hermiller, S. and Šunić, Z., Poly-free constructions for right-angled artin groups, J. Group Theory 10 (2007), 117–138. MR2288463CrossRefGoogle Scholar
Kambites, M., On commuting elements and embeddings of graph groups and monoids, Proc. Edinb. Math. Soc. (2) 52(1) (2009), 155–170. MR2475886CrossRefGoogle Scholar
Kapovich, M. and Millson, J. J., On representation varieties of Artin groups, projective arrangements and the fundamental groups of smooth complex algebraic varieties, Inst. Hautes ÉTudes Sci. Publ. Math. 88 (1998), 5–95. MR1733326CrossRefGoogle Scholar
Kim, S.-H. and Koberda, T., Embedability between right-angled Artin groups, Geom. Topol. 17(1) (2013), 493–530. MR3039768CrossRefGoogle Scholar
Kim, S.-H. and Koberda, T., Free products and the algebraic structure of diffeomorphism groups, J. Topol. 11(4) (2018), 1054–1076. MR3989437CrossRefGoogle Scholar
Koberda, T., Right-angled Artin groups and a generalized isomorphism problem for finitely generated subgroups of mapping class groups, Geom. Funct. Anal. 22(6) (2012), 1541–1590. MR3000498CrossRefGoogle Scholar
Koberda, T., Geometry and combinatorics via right-angled Artin groups, In the tradition of Thurston II, Geometry and groups, (Springer, Cham, 2022). MR4472060Google Scholar
Kotlov, A., Lovász, L. and Vempala, S., The Colin de Verdière number and sphere representations of a graph, Combinatorica 17(4) (1997), 483–521.CrossRefGoogle Scholar
Morey, S. and Villarreal, R. H., Edge ideals: algebraic and combinatorial properties, Progress in commutative algebra, Volume 1, (de Gruyter, Berlin, 2012). MR2932582Google Scholar
O’Neil, P., A short proof of Mac Lane’s planarity theorem, Proc. Amer. Math. Soc. 37 (1973), 617–618. MR313098CrossRefGoogle Scholar
Sabalka, L., On rigidity and the isomorphism problem for tree braid groups, Groups Geom. Dyn. 3(3) (2009), 469–523. MR2516176 (2010g:20074)CrossRefGoogle Scholar
Servatius, H., Automorphisms of graph groups, J. Algebra 126(1) (1989), 34–60. MR1023285 (90m:20043)CrossRefGoogle Scholar
van der Holst, H., Lovász, L. and Schrijver, A., The Colin de Verdière graph parameter, Graph theory and combinatorial biology (Balatonlelle, 1996), Bolyai Society Mathematical Studies, Volume 7, (János Bolyai Mathematical Society, Budapest, 1999). MR1673503Google Scholar
Van Tuyl, A., A beginner’s guide to edge and cover ideals, Monomial ideals, computations and applications, Lecture Notes in Mathematics, Volume 2083, (Springer, Heidelberg, 2013). MR3184120Google Scholar
Van Tuyl, A., Personal communication, 2023.Google Scholar