Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-23T18:50:49.906Z Has data issue: false hasContentIssue false
  • English
  • Français

A remark on the tensor product of two maximal operator spaces

Published online by Cambridge University Press:  20 January 2009

Christian Le Merdy
Christian Le Merdy
Affiliation:
Equipe de Mathématiques, URA CNRS 741, Université de Franche-Comté, F-25030 Besançon Cedex, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a Banach space E, let us denote by Max(E) the largest operator space structure on E. Recently Paulsen-Pisier and, independently, Junge proved that for any Banach spaces E, F, 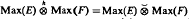isomorphically where 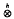and 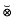respectively denote the Haagerup tensor product and the spatial tensor product of operator spaces. In this paper we show that, in general, this equality does not hold completely isomorphically.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 40 , Issue 2 , June 1997 , pp. 375 - 381
Copyright
Copyright © Edinburgh Mathematical Society 1997

References

REFERENCES

1. Blecher, D., Tensor products of operator spaces II, Canad. J. Math. 44 (1992), 75–90.CrossRefGoogle Scholar
2. Blecher, D., The standard dual of an operator space, Pacific J. Math. 153 (1992), 15–30.CrossRefGoogle Scholar
3. Blecher, D. and Paulsen, V., Tensor products of operator spaces, J. Funct. Anal. 99 (1991), 262–292.CrossRefGoogle Scholar
4. Dvoretsky, A., Some results on convex bodies and Banach spaces, in Proc. Internat. Symp. on linear spaces (Jerusalem, 1961), 123–160.Google Scholar
5. Junge, M. and Pisier, G., Bilinear forms on exact operator spaces and B(H)⊗B(H), Geom. Funct. Anal. 5 (1995), 329–363.CrossRefGoogle Scholar
6. Effros, E. and Ruan, Z.-J., A new approach to operator spaces, Canad. Math. Bull. 34 (1991), 329–337.CrossRefGoogle Scholar
7. Effros, E. and Ruan, Z.-J., Self duality for the Haagerup tensor product and Hilbert space factorization, J. Funct. Anal. 100 (1991), 257–284.CrossRefGoogle Scholar
8. Paulsen, V., Representations of function algebras, abstract operators spaces and Banach space geometry, J. Funct. Anal. 109 (1992), 113–129.CrossRefGoogle Scholar
9. Paulsen, V., The maximal operator space of a normed space, Proc. Edinburgh Math. Soc. 39 (1996), 309–323.CrossRefGoogle Scholar
10. Pisier, G., Factorization of linear operators and geometry of Banach spaces (CBMS Regional Conference Series 60, 1986).CrossRefGoogle Scholar
11. Pisier, G., Similarity problems and completely bounded maps (Lecture Notes 1618, Springer Verlag, 1996).CrossRefGoogle Scholar