Article contents
Regions of the n-sphere and related integrals
Published online by Cambridge University Press: 20 January 2009
Extract
In this note the volumes of certain regions in the n-sphere will be found in two ways: (a) by using a symmetry argument, (b) by expressing the volumes as repeated integrals over the (n-l)-cube. By considering the 4 and 5 spheres and equating the integrals obtained by method (b) to the solution obtained by method (a) we evaluate integrals of the form
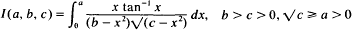
for certain values of a, b and c; it does not appear easy (if indeed it is possible) to evaluate these integrals by direct methods.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 21 , Issue 2 , September 1978 , pp. 129 - 133
- Copyright
- Copyright © Edinburgh Mathematical Society 1978
References
REFERENCES
- 1
- Cited by


