No CrossRef data available.
Article contents
Real Linear Substitutions with Equimodular Multipliers, and their expression in terms of their Invariants
Published online by Cambridge University Press: 20 January 2009
Extract
§1. Let
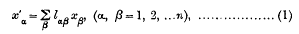
denote a linear substitution of non-vanishing determinant; and let the roots k∈ of its characteristic equation
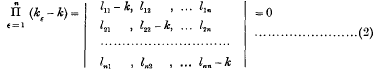
be for the present assumed distinct. Then with each root k∈ is associated an invariant point or pole P∈, and a linear invariant, or invariant (n−2)-plane ξ∈. If the n points P∈ do not lie on an (n−2)-plane, the determinant of their coordinates,
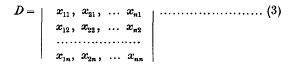
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1916
References
page 20 note * Hilton, , Linear Substitutions, p. 12, Ex. 7.Google Scholar
page 21 note * Scott, , Determinants, p. 81.Google ScholarPubMed
page 21 note † Hilton, ibid., p. 26.
page 28 note * For a case with no real linear invariants, but ½ n real quadratic invariants, see below, § 10.
page 33 note * Salmon-Rogers, , Analytical Geometry of Three Dimensions (1912), §79.Google Scholar
page 33 note † See, e.g., Routh, Advanced Rigid Dynamics, §269.
page 40 note * See also Bell, Coordinate Geometry of Three Dimensions, §§ 166–8; Salmon-Rogers, § 202.


