Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-18T22:20:08.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Radially symmetric solutions of a class of singular elliptic equations

Published online by Cambridge University Press:  20 January 2009

Juan A. Gatica ,
Gaston E. Hernandez  and
P. Waltman
Juan A. Gatica
Affiliation:
Department of Mathematics, University of Iowa, Iowa City, Iowa 52242, U.S.A.
Gaston E. Hernandez
Affiliation:
Department of Mathematics, University of Iowa, Iowa City, Iowa 52242, U.S.A.
P. Waltman
Affiliation:
Department of Mathematics and Computer Science, Emory University, Atlanta, Georgia 30322, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The boundary value problem

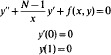
is studied with a view to obtaining the existence of positive solutions in C1([0, 1])∩C2((0, 1)). The function f is assumed to be singular in the second variable, with the singularity modeled after the special case f(x, y) = a(x)y−p, p>0.

This boundary value problem arises in the search of positive radially symmetric solutions to

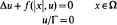
where Ω is the open unit ball in ℝN, centered at the origin, Γ is its boundary and |x| is the Euclidean norm of x.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 33 , Issue 2 , June 1990 , pp. 169 - 180
Copyright
Copyright © Edinburgh Mathematical Society 1990

References

REFERENCES

1.Atkinson, F. V. and Peletier, L. A., Ground states of −Δu = f(u) and the Emden–Fowler equation, Arch. Rational Mech. Anal. 93 (1986), 103–107.CrossRefGoogle Scholar
2.Diaz, J. D., Morel, J. M. and Oswald, L., An elliptic equation with singular nonlinearity, Comm. Partial Differential Equations 12 (1987), 1333–1344.CrossRefGoogle Scholar
3.Erbe, L. and Schmitt, K., On radial solutions of some semilinear elliptic equations, Diff. and Int. Equations 1 (1988), 71–78.Google Scholar
4.Gatica, J. A., Oliker, V. and Waltman, P., Iterative procedures for nonlinear second order boundary value problems (Emory University preprint, 1987).Google Scholar
5.Gatica, J. A., Oliker, V. and Waltman, P., Singular nonlinear boundary value problems for second order differential equations, J. Differential Equations 79 (1989), 62–78.CrossRefGoogle Scholar
6.Gidas, B., Ni, Wei-Ming and Niremberg, L., Symmetry of positive solutions of nonlinear elliptic equations in ℝn, Adv. Math Suppl. Stud. 7A (1981), 369–402.Google Scholar
7.Nachman, A. and Callegari, A., A nonlinear boundary value problem in the theory of pseudoplastic fluids, SIAM J. Appl. Math. 38 (1980), 275–281.CrossRefGoogle Scholar
8.Nussbaum, R. D. and Stuart, C. A., A singular bifurcation problem, J. London Math. Soc. (2) 14 (1976), 31–38.CrossRefGoogle Scholar
9.Oliker, V. I., Near radially symmetric solutions of an inverse problem in geometric optics, Inverse Problems 3 (1987), 743–756.CrossRefGoogle Scholar
10.Stuart, C. A., Concave solutions of singular non-linear differential equations, Math. Z. 136 (1974), 117–135.CrossRefGoogle Scholar
11.Taliaferro, S., A nonlinear singular boundary value problem, Nonlinear Anal. 3 (1979), 897–904.CrossRefGoogle Scholar
12.Wong, J. S. W., On the generalized Emden–Fowler equation, SIAM Rev. 17 (1975), 339–360.CrossRefGoogle Scholar