No CrossRef data available.
Published online by Cambridge University Press: 07 March 2024
In this paper, we mainly prove the following conjectures of Sun [16]: Let p > 3 be a prime. Then \begin{align*}&A_{2p}\equiv A_2-\frac{1648}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\&A_{2p-1}\equiv A_1+\frac{16p^3}3B_{p-3}\ ({\rm{mod}}\ p^4),\\&A_{3p}\equiv A_3-36738p^3B_{p-3}\ ({\rm{mod}}\ p^4),\end{align*}
\begin{align*}&A_{2p}\equiv A_2-\frac{1648}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\&A_{2p-1}\equiv A_1+\frac{16p^3}3B_{p-3}\ ({\rm{mod}}\ p^4),\\&A_{3p}\equiv A_3-36738p^3B_{p-3}\ ({\rm{mod}}\ p^4),\end{align*}
where 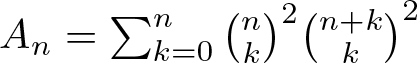 $A_n=\sum_{k=0}^n\binom{n}k^2\binom{n+k}{k}^2$ is the nth Apéry number, and Bn is the nth Bernoulli number.
$A_n=\sum_{k=0}^n\binom{n}k^2\binom{n+k}{k}^2$ is the nth Apéry number, and Bn is the nth Bernoulli number.