Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Howie, J. M.
1977.
Séminaire d’Algèbre Paul Dubreil Paris 1975–1976 (29ème Année).
Vol. 586,
Issue. ,
p.
110.
Molchanov, V. A.
1983.
Semigroups of mappings on graphs.
Semigroup Forum,
Vol. 27,
Issue. 1,
p.
155.
Kowol, G.
and
Mitsch, H.
1986.
Naturally ordered transformation semigroups.
Monatshefte f�r Mathematik,
Vol. 102,
Issue. 2,
p.
115.
Higgins, Peter M.
1990.
Lattices, Semigroups, and Universal Algebra.
p.
89.
Gomes, Gracinda M. S.
and
Howie, John M.
1992.
On the ranks of certain semigroups of order-preserving transformations.
Semigroup Forum,
Vol. 45,
Issue. 1,
p.
272.
Umar, Abdullahi
1992.
On the semigroups of order-decreasing finite full transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 120,
Issue. 1-2,
p.
129.
Umar, Abdullahi
1993.
On the semigroups of partial one-to-one order-decreasing finite transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 123,
Issue. 2,
p.
355.
Higgins, Peter M.
1993.
Combinatorial results for semigroups of order-preserving mappings.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 113,
Issue. 2,
p.
281.
Adams, M. E.
Bulman-Fleming, Sydney
Gould, Matthew
and
Wildsmith, Amy
1994.
Finite semilattices whose non-invertible endomorphisms are products of idempotents.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 124,
Issue. 6,
p.
1193.
Bulman-Fleming, Sydney
1995.
Regularity and products of idempotents in endomorphism monoids of projective acts.
Mathematika,
Vol. 42,
Issue. 2,
p.
354.
Lavers, T. G.
1996.
The monoid of ordered partitions of a natural number.
Semigroup Forum,
Vol. 53,
Issue. 1,
p.
44.
Bulman-Fleming, Sydney
and
Fountain, John
1997.
Products of idempotent endomorphisms of free acts of infinite rank.
Monatshefte f�r Mathematik,
Vol. 124,
Issue. 1,
p.
1.
Lavers, T. G.
1998.
Applications of Fibonacci Numbers.
p.
255.
Yang, Xiuliang
1999.
Products of idempotents of defect 1 in certain semigroups of transformations.
Communications in Algebra,
Vol. 27,
Issue. 7,
p.
3557.
Kemprasit, Yupaporn
and
Changphas, Thawhat
2000.
Regular order-preserving transformation semigroups.
Bulletin of the Australian Mathematical Society,
Vol. 62,
Issue. 3,
p.
511.
Xiuliang, Yang
and
Chunghan, Lu
2000.
Maximal properties of some subsemigroups in finite order-preserving transformation semigroups.
Communications in Algebra,
Vol. 28,
Issue. 7,
p.
3125.
Xiuliang, Yang
2000.
A classification of maximal subsemigroups of finite order-preserving transformation semigroups.
Communications in Algebra,
Vol. 28,
Issue. 3,
p.
1503.
CATARINO, P. M.
and
HIGGINS, P. M.
2002.
THE PSEUDOVARIETY GENERATED BY ALL SEMIGROUPS OF ORIENTATION-PRESERVING TRANSFORMATIONS ON A FINITE CYCLE.
International Journal of Algebra and Computation,
Vol. 12,
Issue. 03,
p.
387.
Barnes, George
and
Levi, Inessa
2003.
Ranks of Semigroups Generated by Order-Preserving Transformations with a Fixed Partition Type.
Communications in Algebra,
Vol. 31,
Issue. 4,
p.
1753.
Laradji, A
and
Umar, A
2004.
Combinatorial results for semigroups of order-preserving partial transformations.
Journal of Algebra,
Vol. 278,
Issue. 1,
p.
342.
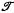 , one of the results being that if X is finite then every element of
, one of the results being that if X is finite then every element of 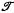 that is not bijective is expressible as a product of idempotents. In view of this it was natural to ask whether by analogy every singular square matrix is expressibleas a product of idempotent matrices. This is indeed the case, as was shown by J. A. Erdos (2). Magill (6) has considered products of idempotents in thesemigroup of all continuous self-maps of a topological space X, but a comparable characterization of products of idempotents in this case appears to be extremelydifficult, and no solution is available yet.
that is not bijective is expressible as a product of idempotents. In view of this it was natural to ask whether by analogy every singular square matrix is expressibleas a product of idempotent matrices. This is indeed the case, as was shown by J. A. Erdos (2). Magill (6) has considered products of idempotents in thesemigroup of all continuous self-maps of a topological space X, but a comparable characterization of products of idempotents in this case appears to be extremelydifficult, and no solution is available yet.

