Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T00:58:05.192Z Has data issue: false hasContentIssue false
  • English
  • Français

The Point Value Maximization Problem for Positive Definite Functions Supported in a Given Subset of a Locally Compact Group

Part of: Locally compact groups and their algebras Harmonic analysis in one variable Abstract harmonic analysis

Published online by Cambridge University Press:  24 January 2018

Sándor Krenedits  and
Szilárd Gy. Révész
Sándor Krenedits*
Affiliation:
Faculty of Mechanical Engineering, Institute of Mathematics and Informatics, St. Stephen University Gödöllő, Páter Károly u. 1. 2100 Hungary ([email protected])
Szilárd Gy. Révész
Affiliation:
Faculty of Sciences, Institute of Mathematics and Informatics, University of Pécs, Pécs, Vasvári Pál utca 4, 7622 Hungary Alfréd Rényi Institute of Mathematics, Hungarian Academy of Sciences Budapest, Reáltanoda utca 13–15. 1053 Hungary ([email protected])
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

The century-old extremal problem, solved by Carathéodory and Fejér, concerns a non-negative trigonometric polynomial 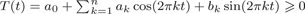$T(t) = a_0 + \sum\nolimits_{k = 1}^n {a_k} \cos (2\pi kt) + b_k\sin (2\pi kt){\ge}0$, normalized by a0=1, where the quantity to be maximized is the coefficient a1 of cos (2π t). Carathéodory and Fejér found that for any given degree n, the maximum is 2 cos(π/n+2). In the complex exponential form, the coefficient sequence (ck) ⊂ ℂ will be supported in [−n, n] and normalized by c0=1. Reformulating, non-negativity of T translates to positive definiteness of the sequence (ck), and the extremal problem becomes a maximization problem for the value at 1 of a normalized positive definite function c: ℤ → ℂ, supported in [−n, n]. Boas and Kac, Arestov, Berdysheva and Berens, Kolountzakis and Révész and, recently, Krenedits and Révész investigated the problem in increasing generality, reaching analogous results for all locally compact abelian groups. We prove an extension to all the known results in not necessarily commutative locally compact groups.

Keywords

Carathéodory–Fejér extremal problemlocally compact topological groupsabstract harmonic analysisHaar measuremodular functionconvolution of functions and of measurespositive definite functionsBochner–Weil theoremconvolution squareFejér–Riesz theorem

MSC classification

Primary: 43A35: Positive definite functions on groups, semigroups, etc. 43A70: Analysis on specific locally compact and other abelian groups
Secondary: 42A05: Trigonometric polynomials, inequalities, extremal problems 42A82: Positive definite functions 22D05: General properties and structure of locally compact groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 1 , February 2018 , pp. 179 - 200
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Arestov, V., Berdysheva, E. and Berens, H., On pointwise Turán's problem for positive definite functions, East J. Approx. 9(1) (2003), 31–42.Google Scholar
2. Bachman, G., Elements of abstract harmonic analysis (Academic Press, New York, London, 1964).Google Scholar
3. Baumgartner, U. and Willis, G. A., Contraction groups and scales of automorphisms of totally disconnected locally compact groups, Israel J. Math. 142 (2004), 221–248.CrossRefGoogle Scholar
4. Boas, R. P. Jr. and Kac, M., Inequalities for Fourier transforms of positive functions, Duke Math. J. 12 (1945), 189–206.Google Scholar
5. Caprace, P.-E. and Monod, N., Decomposing locally compact groups into simple pieces, Math. Proc. Cambridge Philos. Soc. 150(1) (2011), 97–128.CrossRefGoogle Scholar
6. Caprace, P.-E., Reid, C. D. and Willis, G. A., Limits of contraction groups and the Tits core, J. Lie Theory 24(4) (2014), 957–967.Google Scholar
7. Carathéodory, C., Über den Variabilitätsbereich der Fourier'schen Konstanten von positiven harmonischen Funktionen, Rend. Circ. Mat. Palermo 32 (1911), 193–217.CrossRefGoogle Scholar
8. Ehm, W., Gneiting, T. and Richards, D., Convolution roots of radial positive definite functions with compact support, Trans. Amer. Math. Soc. 356(11) (2004), 4655–4685.CrossRefGoogle Scholar
9. Ellis, R., Distal transformation groups, Pacific J. Math. 8 (1958), 401–405.CrossRefGoogle Scholar
10. Fejér, L., Über trigonometrische Polynome, J. Reine Angew. Math. 146 (1915), 53–82.Google Scholar
11. Fejér, L., Gesammelte arbeiten I–II (Akadémiai Kiadó, Budapest, 1970).Google Scholar
12. Folland, G. B., A course in abstract harmonic analysis, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1995).Google Scholar
13. Halmos, P. R., Finite dimensional vector spaces, 2nd edition (Van Nostrand, 1958).Google Scholar
14. Hewitt, E. and Ross, K. A., Abstract harmonic analysis, I, Die Grundlehren der mathemtischen Wissenchaften in Einzeldarstellungen , Volume 115 (Springer, 1963).Google Scholar
15. Hewitt, E. and Ross, K. A., Abstract harmonic analysis, II, Die Grundlehren der mathemtischen Wissenchaften , Volume 152 (Springer, 1970).Google Scholar
16. Ivanov, V. I. and Ivanov, A. V., Turán problems for periodic positive definite functions, Ann. Univ. Sci.Budapest. Sect. Comput. 33 (2010), 219–237.Google Scholar
17. Jaworski, W., On contraction groups of automorphisms of totally disconnected locally compact groups, Israel J. Math. 172 (2009), 1–8.CrossRefGoogle Scholar
18. Kolountzakis, M. N. and Révész, Sz. Gy., On pointwise estimates of positive definite functions with given support, Canad. J. Math. 58(2) (2006), 401–418.CrossRefGoogle Scholar
19. Kolountzakis, M. N. and Révész, Sz. Gy., Turán's extremal problem for positive definite functions on groups, J. Lond. Math. Soc. 74 (2006), 475–496.CrossRefGoogle Scholar
20. Krenedits, S. and Révész, Sz. Gy., Carathéodory–Fejér type extremal problems on locally compact Abelian groups, J. Approx. Theory 194 (2015), 108–131.CrossRefGoogle Scholar
21. Mathias, M., Über Positive Fourier-Integrale, Math. Z. 16 (1923), 103–125 (in German).CrossRefGoogle Scholar
22. Révész, Sz. Gy., Turán's extremal problem on locally compact abelian groups, Anal. Math. 37 (2011) 15–50.CrossRefGoogle Scholar
23. Raja, C. R. E. and Shah, R.. Some properties of distal actions on locally compact groups, Ergodic Theory Dynam. Systems, to appear.Google Scholar
24. Rudin, W., Fourier analysis on groups, Interscience Tracts in Pure and Applied Mathematics , Volume 12 (Interscience Publishers, 1962).Google Scholar
25. Stechkin, S. B., An extremal problem for trigonometric series with nonnegative coefficients, Acta Math. Acad. Sci. Hung. 23(3–4) (1972), 289–291 (in Russian).Google Scholar
26. SzegŐ, G., Orthogonal polynomials, American Mathematical Society Colloquium Publications , Volume XXIII (American Mathematical Society, Providence, RI, 1975).Google Scholar
27. Toeplitz, O., Über die Fourier'sche Entwicklung positiver Funktionen, Rend. Circ. Mat. Palermo 32 (1911), 191–192.CrossRefGoogle Scholar