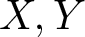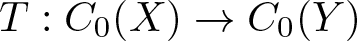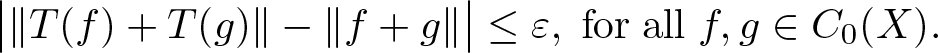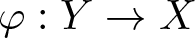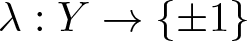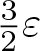1. Introduction
Let X be a locally compact Hausdorff space. The space ![]() $C_0(X)$ will stand for the Banach space of all continuous real-valued functions which vanish at infinity on X (i.e.
$C_0(X)$ will stand for the Banach space of all continuous real-valued functions which vanish at infinity on X (i.e. ![]() $\{x\in X: |f(x)|\geq\varepsilon\}$ is compact in X for every
$\{x\in X: |f(x)|\geq\varepsilon\}$ is compact in X for every ![]() $f\in C_0(X)$ and every ɛ > 0) equipped with the supremum norm. The following result is well-known as the Banach–Stone theorem (see [Reference Banach2, Reference Behrends3, Reference Stone21]).
$f\in C_0(X)$ and every ɛ > 0) equipped with the supremum norm. The following result is well-known as the Banach–Stone theorem (see [Reference Banach2, Reference Behrends3, Reference Stone21]).
Theorem 1.1. Let ![]() $X, Y$ be two locally compact Hausdorff spaces and
$X, Y$ be two locally compact Hausdorff spaces and ![]() $T:C_0(X)\rightarrow C_0(Y)$ be a linear surjective isometry. Then there exists a homeomorphism
$T:C_0(X)\rightarrow C_0(Y)$ be a linear surjective isometry. Then there exists a homeomorphism ![]() $\varphi:Y\rightarrow X$ and a continuous function
$\varphi:Y\rightarrow X$ and a continuous function ![]() $\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that
$\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that
The Banach–Stone theorem describes a deep fact that the linear metric structure of ![]() $C_0(X)$ determines the topology of X. And it has found a large number of generalizations and variants in many different contexts (see [Reference Garrido and Jaramillo15] for a survey of corresponding results). The classical Mazur–Ulam theorem [Reference Mazur and Ulam18] states that every standard surjective isometry between two real Banach spaces must be linear. Thus, the existence of a standard surjective isometry between
$C_0(X)$ determines the topology of X. And it has found a large number of generalizations and variants in many different contexts (see [Reference Garrido and Jaramillo15] for a survey of corresponding results). The classical Mazur–Ulam theorem [Reference Mazur and Ulam18] states that every standard surjective isometry between two real Banach spaces must be linear. Thus, the existence of a standard surjective isometry between ![]() $C_0(X)$ and
$C_0(X)$ and ![]() $C_0(Y)$ can also guarantee that X and Y are homeomorphic. Instead of isometries, Amir and Cambern investigated the linear isomorphisms between
$C_0(Y)$ can also guarantee that X and Y are homeomorphic. Instead of isometries, Amir and Cambern investigated the linear isomorphisms between ![]() $C_0(X)$ and
$C_0(X)$ and ![]() $C_0(Y)$, where
$C_0(Y)$, where ![]() $X, Y$ are compact Hausdorff spaces or locally compact Hausdorff spaces ([Reference Amir1, Reference Cambern5–Reference Cambern7]) . They showed that if the linear isomorphism
$X, Y$ are compact Hausdorff spaces or locally compact Hausdorff spaces ([Reference Amir1, Reference Cambern5–Reference Cambern7]) . They showed that if the linear isomorphism ![]() $T:C_0(X)\rightarrow C_0(Y)$ satisfies that
$T:C_0(X)\rightarrow C_0(Y)$ satisfies that ![]() $\|T\|\cdot\|T^{-1}\| \lt 2$, then the underlying spaces X and Y are homeomorphic, and the universal constant ‘2’ is optimal (see [Reference Cohen9]).
$\|T\|\cdot\|T^{-1}\| \lt 2$, then the underlying spaces X and Y are homeomorphic, and the universal constant ‘2’ is optimal (see [Reference Cohen9]).
In another direction, the nonlinear extension of the Banach–Stone theorem has attracted a large number of mathematicians’ attention (see [Reference Dutrieux and Kalton11–Reference Galego14, Reference Jarosz17, Reference Vestfrid23]). Recently, Galego and Porto da Silva [Reference Galego14] studied the bijective coarse quasi-isometries between ![]() $C_0(X)$ and
$C_0(X)$ and ![]() $C_0(Y)$ and they obtained an optimal nonlinear extension of the Banach–Stone theorem.
$C_0(Y)$ and they obtained an optimal nonlinear extension of the Banach–Stone theorem.
Let ![]() $E, F$ be two Banach spaces. A map
$E, F$ be two Banach spaces. A map ![]() $T:E\rightarrow F$ is said to be a coarse quasi-isometry (or coarse (M,ɛ)-quasi-isometry) for some constants
$T:E\rightarrow F$ is said to be a coarse quasi-isometry (or coarse (M,ɛ)-quasi-isometry) for some constants ![]() $M\geq1$ and
$M\geq1$ and ![]() $\varepsilon\geq0$ provided
$\varepsilon\geq0$ provided
 \begin{equation*}
\frac{1}{M}\|u-v\|-\varepsilon\leq\|T(u)-T(v)\|\leq M\|u-v\|+\varepsilon,
\end{equation*}
\begin{equation*}
\frac{1}{M}\|u-v\|-\varepsilon\leq\|T(u)-T(v)\|\leq M\|u-v\|+\varepsilon,
\end{equation*} for all ![]() $u,v\in E$. T is called an ɛ-isometry when M = 1 and an isometry when M = 1 and ɛ = 0. If
$u,v\in E$. T is called an ɛ-isometry when M = 1 and an isometry when M = 1 and ɛ = 0. If ![]() $T(0)=0$, then T is called standard.
$T(0)=0$, then T is called standard.
Theorem 1.2. (Galego-Porto da Silva)
Let ![]() $X, Y$ be two locally compact Hausdorff spaces and
$X, Y$ be two locally compact Hausdorff spaces and ![]() $T:C_0(X)\rightarrow C_0(Y)$ be a standard bijective map such that both T and T −1 are coarse
$T:C_0(X)\rightarrow C_0(Y)$ be a standard bijective map such that both T and T −1 are coarse ![]() $(M,\varepsilon)$-quasi-isometries with
$(M,\varepsilon)$-quasi-isometries with ![]() $M \lt \sqrt{2}$. Then there exists a homeomorphism
$M \lt \sqrt{2}$. Then there exists a homeomorphism ![]() $\varphi: Y\rightarrow X$ and a continuous function
$\varphi: Y\rightarrow X$ and a continuous function ![]() $\lambda: Y\rightarrow\{\pm1\}$ such that
$\lambda: Y\rightarrow\{\pm1\}$ such that
where Δ does not depend on f and y.
The upper bound ![]() $\sqrt{2}$ on M is optimal even in the linear case when T is a linear isomorphism [Reference Cohen9]. When M = 1, i.e.
$\sqrt{2}$ on M is optimal even in the linear case when T is a linear isomorphism [Reference Cohen9]. When M = 1, i.e. ![]() $T:C_0(X)\rightarrow C_0(Y)$ is a bijective standard ɛ-isometry, Theorem 1.2 yields that
$T:C_0(X)\rightarrow C_0(Y)$ is a bijective standard ɛ-isometry, Theorem 1.2 yields that
As it follows from a result of Omladič and Šemrl [Reference Omladič20], T can be weaken as a standard surjective ɛ-isometry and the estimate ‘2ɛ’ is optimal (see, also, [Reference Benyamini and Lindenstrauss4, p. 360]).
In view of geometry, the isometry T from Banach space E to another Banach space F preserves the length of one diagonal of the parallelogram generated by two vectors. But, one may ask what happens if T preserves the length of another diagonal of the parallelogram instead, that is,
By letting ![]() $g=-f$ in the above equation, it is clear that T is an isometry with
$g=-f$ in the above equation, it is clear that T is an isometry with ![]() $T(-f)=-T(f)$ and
$T(-f)=-T(f)$ and ![]() $T(0)=0$. Thus, the Banach–Stone theorem (Theorem 1.1) still holds when T is surjective. Such transformations are called norm-additive maps and have stronger properties than isometries when the domain is symmetric. And these maps have been studied recently in [Reference Chen, Dong and Zheng8, Reference Dong, Li, Molnár and Wong10, Reference Hosseini and Font16, Reference Molnár19, Reference Tonev and Yates22].
$T(0)=0$. Thus, the Banach–Stone theorem (Theorem 1.1) still holds when T is surjective. Such transformations are called norm-additive maps and have stronger properties than isometries when the domain is symmetric. And these maps have been studied recently in [Reference Chen, Dong and Zheng8, Reference Dong, Li, Molnár and Wong10, Reference Hosseini and Font16, Reference Molnár19, Reference Tonev and Yates22].
Let ![]() $E, F$ be two Banach spaces and
$E, F$ be two Banach spaces and ![]() $T:E\rightarrow F$ be a map,
$T:E\rightarrow F$ be a map, ![]() $\varepsilon\geq0$. T is called an ɛ-norm-additive map provided
$\varepsilon\geq0$. T is called an ɛ-norm-additive map provided
 \begin{equation*}
\big|\|T(u)+T(v)\|-\|u+v\|\big|\leq \varepsilon,\;{\rm for\;all}\; u, v\in E.
\end{equation*}
\begin{equation*}
\big|\|T(u)+T(v)\|-\|u+v\|\big|\leq \varepsilon,\;{\rm for\;all}\; u, v\in E.
\end{equation*} In this paper, we mainly study the properties of the ɛ-norm-additive map between ![]() $C_0(X)$ and
$C_0(X)$ and ![]() $C_0(Y)$ which is a natural and interesting generalization of norm-additive map to the perturbed case. It is worth noting that although the proof of Theorem 1.2 for the sharp estimate ‘2ɛ’ of the surjective ɛ-isometries is very skilful [Reference Galego14], it cannot be applied to ɛ-norm-additive mappings for hunting the sharp estimate because the ɛ-norm-additive mapping between
$C_0(Y)$ which is a natural and interesting generalization of norm-additive map to the perturbed case. It is worth noting that although the proof of Theorem 1.2 for the sharp estimate ‘2ɛ’ of the surjective ɛ-isometries is very skilful [Reference Galego14], it cannot be applied to ɛ-norm-additive mappings for hunting the sharp estimate because the ɛ-norm-additive mapping between ![]() $C_0(X)$ and
$C_0(X)$ and ![]() $C_0(Y)$ may be a strictly 2ɛ-isometry (see Example 2.3).
$C_0(Y)$ may be a strictly 2ɛ-isometry (see Example 2.3).
We mainly prove that if ![]() $X, Y$ are two locally compact Hausdorff spaces and
$X, Y$ are two locally compact Hausdorff spaces and ![]() $T:C_0(X)\rightarrow C_0(Y)$ is a standard surjective ɛ-norm-additive map, then there exists a homeomorphism
$T:C_0(X)\rightarrow C_0(Y)$ is a standard surjective ɛ-norm-additive map, then there exists a homeomorphism ![]() $\varphi:Y\rightarrow X$ and a continuous function
$\varphi:Y\rightarrow X$ and a continuous function ![]() $\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that
$\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that
 \begin{equation*}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\;y\in Y,\;f\in C_0(X).
\end{equation*}
\begin{equation*}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\;y\in Y,\;f\in C_0(X).
\end{equation*} The constant ‘![]() $\frac{3}{2}$’ is optimal.
$\frac{3}{2}$’ is optimal.
2. Main results
We start this section with the following observation which reveals the relationship between ɛ-isometries and ɛ-norm-additive maps on Banach spaces.
Proposition 2.1. Suppose that E and F are Banach spaces and ![]() $T:E\rightarrow F$ is an ɛ-norm-additive map. Then T is a 2ɛ-isometry.
$T:E\rightarrow F$ is an ɛ-norm-additive map. Then T is a 2ɛ-isometry.
Proof. For any ![]() $u\in E$, by the definition of T, we have
$u\in E$, by the definition of T, we have
 \begin{equation*}
\big|\|T(u)+T(-u)\|-\|u-u\|\big|\leq\varepsilon,
\end{equation*}
\begin{equation*}
\big|\|T(u)+T(-u)\|-\|u-u\|\big|\leq\varepsilon,
\end{equation*}i.e.
For ![]() $u,v\in E$, we obtain that
$u,v\in E$, we obtain that
 \begin{align*}
\|T(u)-T(v)\|&=\|(T(u)+T(-u))-(T(-u)+T(v))\|\\
&\leq \|T(-u)+T(v)\|+\|T(u)+T(-u)\|\\
&\leq\|u-v\|+2\varepsilon,
\end{align*}
\begin{align*}
\|T(u)-T(v)\|&=\|(T(u)+T(-u))-(T(-u)+T(v))\|\\
&\leq \|T(-u)+T(v)\|+\|T(u)+T(-u)\|\\
&\leq\|u-v\|+2\varepsilon,
\end{align*}and
 \begin{align*}
\|T(u)-T(v)\|&=\|(T(u)+T(-u))-(T(-u)+T(v))\|\\
&\geq\|T(-u)+T(v)\|-\|T(u)+T(-v)\|\\
&\geq\|u-v\|-2\varepsilon.
\end{align*}
\begin{align*}
\|T(u)-T(v)\|&=\|(T(u)+T(-u))-(T(-u)+T(v))\|\\
&\geq\|T(-u)+T(v)\|-\|T(u)+T(-v)\|\\
&\geq\|u-v\|-2\varepsilon.
\end{align*}Thus, T is a 2ɛ-isometry and the proof is complete.
Although every ɛ-norm-additive map is actually a 2ɛ-isometry, the converse is not true in general.
Example 2.2. Define ![]() $T:c_0\rightarrow c_0$ by
$T:c_0\rightarrow c_0$ by ![]() $T(u)=(\|u\|,u_1,u_2,\ldots)$ for
$T(u)=(\|u\|,u_1,u_2,\ldots)$ for ![]() $u=(u_n)_{n=1}^\infty\in c_0$. Then T is a standard (0−)isometry, but it is not a δ-norm-additive map for any
$u=(u_n)_{n=1}^\infty\in c_0$. Then T is a standard (0−)isometry, but it is not a δ-norm-additive map for any ![]() $\delta\geq0$.
$\delta\geq0$.
The following example shows that the constant ‘2’ in Proposition 2.1 is sharp.
Example 2.3. Let ![]() $X=\lbrace a\rbrace$, then
$X=\lbrace a\rbrace$, then ![]() $C(X)=\mathbb{R}$. Fix ɛ > 0, define
$C(X)=\mathbb{R}$. Fix ɛ > 0, define ![]() $T:\mathbb{R}\rightarrow\mathbb{R}$ by
$T:\mathbb{R}\rightarrow\mathbb{R}$ by
 \begin{equation*}T(u)=\begin{cases}
0&\text{if\; \textit{u}\,=\,0},\\
-\frac{\varepsilon}{2}&\text{if\;$u=\varepsilon$},\\
u+\frac{\varepsilon}{2}&\text{if\;$u\neq 0,\varepsilon$}.
\end{cases}\end{equation*}
\begin{equation*}T(u)=\begin{cases}
0&\text{if\; \textit{u}\,=\,0},\\
-\frac{\varepsilon}{2}&\text{if\;$u=\varepsilon$},\\
u+\frac{\varepsilon}{2}&\text{if\;$u\neq 0,\varepsilon$}.
\end{cases}\end{equation*} Then T is a standard ɛ-norm-additive map. Note that  $\big||T(2\varepsilon)-T(\varepsilon)|-|2\varepsilon-\varepsilon|\big|=2\varepsilon$. This and Proposition 2.1 together show that T is a strictly 2ɛ-isometry.
$\big||T(2\varepsilon)-T(\varepsilon)|-|2\varepsilon-\varepsilon|\big|=2\varepsilon$. This and Proposition 2.1 together show that T is a strictly 2ɛ-isometry.
Let ![]() $X, Y$ be two locally compact Hausdorff spaces and
$X, Y$ be two locally compact Hausdorff spaces and ![]() $T:C_0(X)\rightarrow C_0(Y)$ be a standard surjective ɛ-norm-additive map. Combining Proposition 2.1, Theorem 1.2 and the Omladič–Šemrl’s theorem [Reference Omladič20], we have the following result.
$T:C_0(X)\rightarrow C_0(Y)$ be a standard surjective ɛ-norm-additive map. Combining Proposition 2.1, Theorem 1.2 and the Omladič–Šemrl’s theorem [Reference Omladič20], we have the following result.
Theorem 2.4. Let ![]() $T:C_0(X)\rightarrow C_0(Y)$ be a standard surjective ɛ-norm-additive map. Then there exists a homeomorphism
$T:C_0(X)\rightarrow C_0(Y)$ be a standard surjective ɛ-norm-additive map. Then there exists a homeomorphism ![]() $\varphi:Y\rightarrow X$ and a continuous function
$\varphi:Y\rightarrow X$ and a continuous function ![]() $\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that
$\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that
However, the constant in the estimate above is not the best. Our main goal is to obtain a sharp version of the above theorem by reducing 4ɛ to ![]() $\frac{3}{2}\varepsilon$. And then we will show that
$\frac{3}{2}\varepsilon$. And then we will show that ![]() $\frac{3}{2}\varepsilon$ is optimal. To begin with, we establish the following useful lemmas.
$\frac{3}{2}\varepsilon$ is optimal. To begin with, we establish the following useful lemmas.
Lemma 2.5. Let ![]() $x\in X$ and
$x\in X$ and ![]() $f_1, f_2, ..., f_n\in C_0(X)$ with
$f_1, f_2, ..., f_n\in C_0(X)$ with ![]() $(f_1(x),f_2(x),...,f_n(x))\neq 0$. Then there exists a
$(f_1(x),f_2(x),...,f_n(x))\neq 0$. Then there exists a ![]() $g\in C_0(X)$ with
$g\in C_0(X)$ with ![]() $g(z)\leq 0$ for all
$g(z)\leq 0$ for all ![]() $z\in X$ such that
$z\in X$ such that
Proof. Let ![]() $I=[-\|f_1\|,\;\|f_1\|]\times[-\|f_2\|,\;\|f_2\|]\times...\times[-\|f_n\|,\;\|f_n\|]\subset\mathbb{R}^n$. Define
$I=[-\|f_1\|,\;\|f_1\|]\times[-\|f_2\|,\;\|f_2\|]\times...\times[-\|f_n\|,\;\|f_n\|]\subset\mathbb{R}^n$. Define ![]() $F:X\rightarrow \mathbb{R}^n$ by
$F:X\rightarrow \mathbb{R}^n$ by
Then F is well defined and continuous. Let  $\alpha=\max\limits_{1\leq i\leq n}\|f_i\|$. For every
$\alpha=\max\limits_{1\leq i\leq n}\|f_i\|$. For every ![]() $(u_1,u_2,...,u_n)\in I$, let
$(u_1,u_2,...,u_n)\in I$, let
 \begin{equation*}
h((u_1,u_2,...,u_n))=\max\limits_{1\leq i\leq n} \lbrace f_i(x)-u_i-3\alpha, -3\alpha\rbrace.
\end{equation*}
\begin{equation*}
h((u_1,u_2,...,u_n))=\max\limits_{1\leq i\leq n} \lbrace f_i(x)-u_i-3\alpha, -3\alpha\rbrace.
\end{equation*} Then ![]() $h:I\rightarrow \mathbb{R}$ is well defined. It is clear that h is continuous and
$h:I\rightarrow \mathbb{R}$ is well defined. It is clear that h is continuous and ![]() $-3\alpha\leq h(F(z))\leq 0$ for every
$-3\alpha\leq h(F(z))\leq 0$ for every ![]() $z\in X$. By the Urysohn lemma, there exists a continuous function
$z\in X$. By the Urysohn lemma, there exists a continuous function ![]() $P: I\rightarrow [0,1]$ such that
$P: I\rightarrow [0,1]$ such that ![]() $P((0,0,...,0))=0$ and
$P((0,0,...,0))=0$ and ![]() $P(F(x))=1$. Define
$P(F(x))=1$. Define ![]() $g:X\rightarrow \mathbb{R}$ by
$g:X\rightarrow \mathbb{R}$ by
Then g is well defined. Since ![]() $P, h, F$ are continuous, g is also continuous.
$P, h, F$ are continuous, g is also continuous.
We assert that ![]() $g\in C_0(X)$. For any convergent net
$g\in C_0(X)$. For any convergent net ![]() $\lbrace x_\lambda\rbrace_{\lambda\in\Lambda}$ with xλ converges to infinity, we have
$\lbrace x_\lambda\rbrace_{\lambda\in\Lambda}$ with xλ converges to infinity, we have ![]() $ F(x_\lambda)\rightarrow (0,0,...,0)\in\mathbb{R}^n$. Hence
$ F(x_\lambda)\rightarrow (0,0,...,0)\in\mathbb{R}^n$. Hence ![]() $ P(F(x_\lambda))\rightarrow 0$. Note that
$ P(F(x_\lambda))\rightarrow 0$. Note that ![]() $|h(F(x_\lambda))|\leq 3\alpha$ for any
$|h(F(x_\lambda))|\leq 3\alpha$ for any ![]() $\lambda\in\Lambda$, we have
$\lambda\in\Lambda$, we have ![]() $g(x_\lambda)\rightarrow 0$. Thus
$g(x_\lambda)\rightarrow 0$. Thus ![]() $g\in C_0(X)$.
$g\in C_0(X)$.
For every ![]() $z\in X$,
$z\in X$, ![]() $0\leq P(F(z))\leq 1$ and
$0\leq P(F(z))\leq 1$ and ![]() $-3\alpha\leq h(F(z))\leq 0$. Thus
$-3\alpha\leq h(F(z))\leq 0$. Thus ![]() $-3\alpha\leq g(z)\leq 0$ for every
$-3\alpha\leq g(z)\leq 0$ for every ![]() $z\in X$. Note that
$z\in X$. Note that ![]() $g(x)=-3\alpha$, then
$g(x)=-3\alpha$, then ![]() $\|g\|=-g(x)$. For every
$\|g\|=-g(x)$. For every ![]() $i\in\lbrace 1,2,...,n\rbrace$ and every
$i\in\lbrace 1,2,...,n\rbrace$ and every ![]() $z\in X$, we have
$z\in X$, we have
 \begin{align*}
\alpha&\geq g(z)+f_i(z)=P(F(z))\cdot h(F(z))+f_i(z)\\
&\geq h(F(z))+f_i(z)\geq f_i(x)-f_i(z)-3\alpha+f_i(z)\\
&=f_i(x)-3\alpha=g(x)+f_i(x).
\end{align*}
\begin{align*}
\alpha&\geq g(z)+f_i(z)=P(F(z))\cdot h(F(z))+f_i(z)\\
&\geq h(F(z))+f_i(z)\geq f_i(x)-f_i(z)-3\alpha+f_i(z)\\
&=f_i(x)-3\alpha=g(x)+f_i(x).
\end{align*}Then
This implies that ![]() $\|g+f_i\|=-g(x)-f_i(x)$ and the proof is complete.
$\|g+f_i\|=-g(x)-f_i(x)$ and the proof is complete.
Similar to Lemma 2.5, we have the following lemma.
Lemma 2.6. Let ![]() $x\in X$ and
$x\in X$ and ![]() $f_1, f_2, ..., f_n\in C_0(X)$ with
$f_1, f_2, ..., f_n\in C_0(X)$ with ![]() $(f_1(x),f_2(x),...,f_n(x))\neq 0$. Then there exists a
$(f_1(x),f_2(x),...,f_n(x))\neq 0$. Then there exists a ![]() $g\in C_0(X)$ with
$g\in C_0(X)$ with ![]() $g(z)\geq 0$ for all
$g(z)\geq 0$ for all ![]() $z\in X$ such that
$z\in X$ such that
For every ![]() $x\in X$ and
$x\in X$ and ![]() $f\in C_0(X)$, let
$f\in C_0(X)$, let
 \begin{align*}
P(f,x)&=\lbrace (y,\lambda)\in Y\times\lbrace\pm1\rbrace:\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon\rbrace,\\
\bar{P}(f,x)&=\lbrace (y,\lambda)\in Y\times\lbrace\pm1\rbrace:\lambda T(f)(y)\leq f(x)+\frac{3}{2}\varepsilon\rbrace.
\end{align*}
\begin{align*}
P(f,x)&=\lbrace (y,\lambda)\in Y\times\lbrace\pm1\rbrace:\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon\rbrace,\\
\bar{P}(f,x)&=\lbrace (y,\lambda)\in Y\times\lbrace\pm1\rbrace:\lambda T(f)(y)\leq f(x)+\frac{3}{2}\varepsilon\rbrace.
\end{align*}Put
 \begin{equation*}
P_+(x)=\cap_{f\in C_0(X),\;f(x)\geq 0}P(f,x),\;P_-(x)=\cap_{f\in C_0(X),\;f(x)\leq 0}\bar{P}(f,x).
\end{equation*}
\begin{equation*}
P_+(x)=\cap_{f\in C_0(X),\;f(x)\geq 0}P(f,x),\;P_-(x)=\cap_{f\in C_0(X),\;f(x)\leq 0}\bar{P}(f,x).
\end{equation*}Lemma 2.7. For every ![]() $x\in X$,
$x\in X$, ![]() $P_+(x)$ is non-empty.
$P_+(x)$ is non-empty.
Proof. Fix ![]() $x\in X$, the proof is divided into three steps.
$x\in X$, the proof is divided into three steps.
Step I. We prove that for ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with  $f(x) \gt \frac{3}{2}\varepsilon$,
$f(x) \gt \frac{3}{2}\varepsilon$, ![]() $P(f,x)$ is a non-empty compact set. Let
$P(f,x)$ is a non-empty compact set. Let
 \begin{align*}
P_1=\lbrace y\in Y:T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon\rbrace,\;\;
P_2=\lbrace y\in Y:-T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon\rbrace.
\end{align*}
\begin{align*}
P_1=\lbrace y\in Y:T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon\rbrace,\;\;
P_2=\lbrace y\in Y:-T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon\rbrace.
\end{align*}Since T is an ɛ-norm-additive map,
 \begin{equation*}
2\big|\|T(f)\|-\|f\|\big|=\big|\|T(f)+T(f)\|-\|f+f\|\big|\leq \varepsilon,
\end{equation*}
\begin{equation*}
2\big|\|T(f)\|-\|f\|\big|=\big|\|T(f)+T(f)\|-\|f+f\|\big|\leq \varepsilon,
\end{equation*}i.e.
 \begin{equation*}\|f\|-\frac{1}{2}\varepsilon\leq\|T(f)\|\leq \|f\|+\frac{1}{2}\varepsilon.\end{equation*}
\begin{equation*}\|f\|-\frac{1}{2}\varepsilon\leq\|T(f)\|\leq \|f\|+\frac{1}{2}\varepsilon.\end{equation*} This yields that at least one of the ![]() $P_1,\;P_2$ is non-empty. Note that
$P_1,\;P_2$ is non-empty. Note that  $f(x) \gt \frac{3}{2}\varepsilon$, P 1 and P 2 are two compact sets. Since
$f(x) \gt \frac{3}{2}\varepsilon$, P 1 and P 2 are two compact sets. Since ![]() $P(f,x)=P_1\times\lbrace 1\rbrace\cup P_2\times\lbrace -1\rbrace$,
$P(f,x)=P_1\times\lbrace 1\rbrace\cup P_2\times\lbrace -1\rbrace$, ![]() $P(f,x)$ is a non-empty compact subset of
$P(f,x)$ is a non-empty compact subset of ![]() $Y\times \lbrace\pm1\rbrace$.
$Y\times \lbrace\pm1\rbrace$.
Step II. Fix a ![]() $f_0\in C_0(X)$ with
$f_0\in C_0(X)$ with  $f_0(x) \gt \frac{3}{2}\varepsilon$, we prove that
$f_0(x) \gt \frac{3}{2}\varepsilon$, we prove that ![]() $P(f_0,x)\cap P(f,x)$ is a non-empty compact set for every
$P(f_0,x)\cap P(f,x)$ is a non-empty compact set for every ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with ![]() $f(x)\geq 0$. It is clear that
$f(x)\geq 0$. It is clear that ![]() $P(f,x)$ is closed in
$P(f,x)$ is closed in ![]() $Y\times \lbrace\pm1\rbrace$ and hence
$Y\times \lbrace\pm1\rbrace$ and hence ![]() $(P(f_0,x)\cap P(f,x))\subset P(f_0,x)$ is compact. It remains to prove that
$(P(f_0,x)\cap P(f,x))\subset P(f_0,x)$ is compact. It remains to prove that ![]() $P(f_0,x)\cap P(f,x)$ is non-empty. By Lemma 2.5, there exists a
$P(f_0,x)\cap P(f,x)$ is non-empty. By Lemma 2.5, there exists a ![]() $g\in C_0(X)$ such that
$g\in C_0(X)$ such that
Since T is an ɛ-norm-additive map, one has
 \begin{equation*}
\|T(g)\|\geq \|g\|-\frac{1}{2}\varepsilon,\;\|f+g\|+\varepsilon\geq \|T(f)+T(g)\|,\;\|f_0+g\|+\varepsilon\geq \|T(f_0)+T(g)\|.
\end{equation*}
\begin{equation*}
\|T(g)\|\geq \|g\|-\frac{1}{2}\varepsilon,\;\|f+g\|+\varepsilon\geq \|T(f)+T(g)\|,\;\|f_0+g\|+\varepsilon\geq \|T(f_0)+T(g)\|.
\end{equation*} Pick ![]() $(y,\lambda)\in Y\times\lbrace\pm1\rbrace$ such that
$(y,\lambda)\in Y\times\lbrace\pm1\rbrace$ such that ![]() $\|T(g)\|=\lambda T(g)(y)$. Then
$\|T(g)\|=\lambda T(g)(y)$. Then
 \begin{align*}
-g(x)-f_0(x)+\varepsilon&=\|g+f_0\|+\varepsilon\geq\|T(g)+T(f_0)\|\geq \lambda T(g)(y)+\lambda T(f_0)(y)\\
&\geq\|g\|-\frac{1}{2}\varepsilon+\lambda T(f_0)(y)=-g(x)-\frac{1}{2}\varepsilon+\lambda T(f_0)(y).
\end{align*}
\begin{align*}
-g(x)-f_0(x)+\varepsilon&=\|g+f_0\|+\varepsilon\geq\|T(g)+T(f_0)\|\geq \lambda T(g)(y)+\lambda T(f_0)(y)\\
&\geq\|g\|-\frac{1}{2}\varepsilon+\lambda T(f_0)(y)=-g(x)-\frac{1}{2}\varepsilon+\lambda T(f_0)(y).
\end{align*} This implies  $-\lambda T(f_0)(y)\geq f_0(x)-\frac{3}{2}\varepsilon$. Similarly, we can get
$-\lambda T(f_0)(y)\geq f_0(x)-\frac{3}{2}\varepsilon$. Similarly, we can get  $-\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon$. Thus
$-\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon$. Thus ![]() $(y,-\lambda)\in P(f_0,x)\cap P(f,x)$ and
$(y,-\lambda)\in P(f_0,x)\cap P(f,x)$ and ![]() $P(f_0,x)\cap P(f,x)$ is a non-empty compact subset of
$P(f_0,x)\cap P(f,x)$ is a non-empty compact subset of ![]() $Y\times \lbrace\pm1\rbrace$.
$Y\times \lbrace\pm1\rbrace$.
Step III. We prove that the set family ![]() $\lbrace P(f,x)\cap P(f_0,x)\rbrace_{f\in C_0(X),\;f(x)\geq 0}$ has the finite intersection property. Fix
$\lbrace P(f,x)\cap P(f_0,x)\rbrace_{f\in C_0(X),\;f(x)\geq 0}$ has the finite intersection property. Fix ![]() $f_1,f_2,...,f_n\in C_0(X)$ with
$f_1,f_2,...,f_n\in C_0(X)$ with ![]() $f_i(x)\geq 0$ for every
$f_i(x)\geq 0$ for every ![]() $i\in\{1,2,...,n\}$, by Lemma 2.5, there exists a
$i\in\{1,2,...,n\}$, by Lemma 2.5, there exists a ![]() $g\in C_0(X)$ such that
$g\in C_0(X)$ such that
Pick ![]() $(y,\lambda)\in Y\times\lbrace\pm1\rbrace$ such that
$(y,\lambda)\in Y\times\lbrace\pm1\rbrace$ such that ![]() $\|T(g)\|=\lambda T(g)(y)$. For every
$\|T(g)\|=\lambda T(g)(y)$. For every ![]() $i\in\{1,2,...,n\}$, by the same argument as in Step II, we obtain
$i\in\{1,2,...,n\}$, by the same argument as in Step II, we obtain
Thus
Note that
The proof is complete.
The following Lemma 2.8 is analogous to Lemma 2.7 and we omit its proof.
Lemma 2.8. For every ![]() $x\in X$,
$x\in X$, ![]() $P_-(x)$ is non-empty.
$P_-(x)$ is non-empty.
Remark 2.9. Fix ![]() $x\in X$, it is not difficult to verify that if
$x\in X$, it is not difficult to verify that if ![]() $(y,\lambda)\in P_+(x)$, then
$(y,\lambda)\in P_+(x)$, then ![]() $(y,-\lambda)\notin P_+(x)$. Suppose on the contrary that
$(y,-\lambda)\notin P_+(x)$. Suppose on the contrary that ![]() $(y,\lambda), (y,-\lambda)\in P_+(x)$, pick
$(y,\lambda), (y,-\lambda)\in P_+(x)$, pick ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with  $f(x) \gt \frac{3}{2}\varepsilon$, then
$f(x) \gt \frac{3}{2}\varepsilon$, then
 \begin{align*}
\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon \gt 0,\;\;
-\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon \gt 0.
\end{align*}
\begin{align*}
\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon \gt 0,\;\;
-\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon \gt 0.
\end{align*} This leads to a contradiction. By a similar argument as above, we can see that if ![]() $(y,\lambda)\in P_-(x)$, then
$(y,\lambda)\in P_-(x)$, then ![]() $(y,-\lambda)\notin P_-(x)$.
$(y,-\lambda)\notin P_-(x)$.
From now on, we assume that ![]() $T: C_0(X)\rightarrow C_0(Y)$ is a standard surjective ɛ-norm-additive map. For every
$T: C_0(X)\rightarrow C_0(Y)$ is a standard surjective ɛ-norm-additive map. For every ![]() $y\in Y$ and
$y\in Y$ and ![]() $g\in C_0(Y)$, define
$g\in C_0(Y)$, define
 \begin{align*}
Q(g,y)&=\lbrace (x,\lambda)\in X\times\lbrace\pm1\rbrace:\lambda f(x)\geq g(y)-\frac{3}{2}\varepsilon,\;f\in T^{-1}(g)\rbrace,\\
\bar{Q}(g,y)&=\lbrace (x,\lambda)\in X\times\lbrace\pm1\rbrace:\lambda f(x)\leq g(y)+\frac{3}{2}\varepsilon,\;f\in T^{-1}(g)\rbrace.
\end{align*}
\begin{align*}
Q(g,y)&=\lbrace (x,\lambda)\in X\times\lbrace\pm1\rbrace:\lambda f(x)\geq g(y)-\frac{3}{2}\varepsilon,\;f\in T^{-1}(g)\rbrace,\\
\bar{Q}(g,y)&=\lbrace (x,\lambda)\in X\times\lbrace\pm1\rbrace:\lambda f(x)\leq g(y)+\frac{3}{2}\varepsilon,\;f\in T^{-1}(g)\rbrace.
\end{align*}Put
 \begin{equation*}
Q_+(y)=\cap_{g\in C_0(Y),\;g(y)\geq 0}Q(g,y), \;Q_-(y)=\cap_{g\in C_0(Y),\;g(y)\leq 0}\bar{Q}(g,y).
\end{equation*}
\begin{equation*}
Q_+(y)=\cap_{g\in C_0(Y),\;g(y)\geq 0}Q(g,y), \;Q_-(y)=\cap_{g\in C_0(Y),\;g(y)\leq 0}\bar{Q}(g,y).
\end{equation*}Lemma 2.10. For every ![]() $y\in Y$,
$y\in Y$, ![]() $Q_+(y),\;Q_-(y)$ both are non-empty.
$Q_+(y),\;Q_-(y)$ both are non-empty.
Proof. Let ![]() $y\in Y$, we just prove
$y\in Y$, we just prove ![]() $Q_+(y)$ is non-empty, the case for
$Q_+(y)$ is non-empty, the case for ![]() $ Q_-(y)$ is similar. The proof is divided into three steps.
$ Q_-(y)$ is similar. The proof is divided into three steps.
Step I. Assume that ![]() $g\in C_0(Y)$ with
$g\in C_0(Y)$ with  $g(y) \gt \frac{3}{2}\varepsilon$. We first prove
$g(y) \gt \frac{3}{2}\varepsilon$. We first prove ![]() $Q(g,y)$ is a non-empty compact set. By Lemma 2.5, there exists
$Q(g,y)$ is a non-empty compact set. By Lemma 2.5, there exists ![]() $\bar{g}\in C_0(Y)$ such that
$\bar{g}\in C_0(Y)$ such that
Since T is surjective, there exists ![]() $h\in C_0(X)$ such that
$h\in C_0(X)$ such that ![]() $T(h)=\bar{g}$. Find
$T(h)=\bar{g}$. Find ![]() $(x,\lambda)\in X\times\{\pm 1\}$ such that
$(x,\lambda)\in X\times\{\pm 1\}$ such that ![]() $\|h\|=\lambda h(x)$. For every
$\|h\|=\lambda h(x)$. For every ![]() $f\in T^{-1}(g)$,
$f\in T^{-1}(g)$,
 \begin{align*}
\|\bar{g}\|-\frac{1}{2}\varepsilon+\lambda f(x)&\leq\|h\|+\lambda f(x)=\lambda (h(x)+f(x))\\
&\leq\|h+f\|\leq\|T(h)+T(f)\|+\varepsilon\\
&=\|\bar{g}+g\|+\varepsilon=-\bar{g}(y)-g(y)+\varepsilon\\
&=\|\bar{g}\|-g(y)+\varepsilon.
\end{align*}
\begin{align*}
\|\bar{g}\|-\frac{1}{2}\varepsilon+\lambda f(x)&\leq\|h\|+\lambda f(x)=\lambda (h(x)+f(x))\\
&\leq\|h+f\|\leq\|T(h)+T(f)\|+\varepsilon\\
&=\|\bar{g}+g\|+\varepsilon=-\bar{g}(y)-g(y)+\varepsilon\\
&=\|\bar{g}\|-g(y)+\varepsilon.
\end{align*} Thus  $-\lambda f(x)\geq g(y)-\frac{3}{2}\varepsilon$. This implies that
$-\lambda f(x)\geq g(y)-\frac{3}{2}\varepsilon$. This implies that ![]() $(x,-\lambda)\in Q(g,y)$ and
$(x,-\lambda)\in Q(g,y)$ and ![]() $Q(g,y)$ is non-empty. For every
$Q(g,y)$ is non-empty. For every ![]() $f\in T^{-1}(g)$, let
$f\in T^{-1}(g)$, let
 \begin{align*}
R(f)_1=\{x\in X:f(x)\geq g(y)-\frac{3}{2}\varepsilon\},\;\;
R(f)_2=\{x\in X:-f(x)\geq g(y)-\frac{3}{2}\varepsilon\},
\end{align*}
\begin{align*}
R(f)_1=\{x\in X:f(x)\geq g(y)-\frac{3}{2}\varepsilon\},\;\;
R(f)_2=\{x\in X:-f(x)\geq g(y)-\frac{3}{2}\varepsilon\},
\end{align*} \begin{equation*}
R(f)=\{(x,\lambda)\in X\times\lbrace\pm1\rbrace:\lambda f(x)\geq g(y)-\frac{3}{2}\varepsilon\}.
\end{equation*}
\begin{equation*}
R(f)=\{(x,\lambda)\in X\times\lbrace\pm1\rbrace:\lambda f(x)\geq g(y)-\frac{3}{2}\varepsilon\}.
\end{equation*} By the above argument, ![]() $R(f)\neq\emptyset$ and
$R(f)\neq\emptyset$ and ![]() $R(f)=R(f)_1\times \{1\}\cup R(f)_2\times\{-1\}$. Since
$R(f)=R(f)_1\times \{1\}\cup R(f)_2\times\{-1\}$. Since  $g(y) \gt \frac{3}{2}\varepsilon$,
$g(y) \gt \frac{3}{2}\varepsilon$, ![]() $R(f)_1,\;R(f)_2$ are compact. By the Tychonoff theorem, R(f) is a non-empty compact subset of
$R(f)_1,\;R(f)_2$ are compact. By the Tychonoff theorem, R(f) is a non-empty compact subset of ![]() $X\times \lbrace\pm1\rbrace$. Note that
$X\times \lbrace\pm1\rbrace$. Note that  $Q(g,y)=\cap_{f\in T^{-1}(g)}R(f)$, this implies that
$Q(g,y)=\cap_{f\in T^{-1}(g)}R(f)$, this implies that ![]() $Q(g,y)$ is a non-empty compact set.
$Q(g,y)$ is a non-empty compact set.
Step II. Fix ![]() $g_0\in C_0(Y)$ with
$g_0\in C_0(Y)$ with  $g_0(y) \gt \frac{3}{2}\varepsilon$, we will show that for every
$g_0(y) \gt \frac{3}{2}\varepsilon$, we will show that for every ![]() $g\in C_0(Y)$ with
$g\in C_0(Y)$ with ![]() $g(y)\geq 0$,
$g(y)\geq 0$, ![]() $Q(g_0,y)\cap Q(g,y)$ is a non-empty compact set. Note that
$Q(g_0,y)\cap Q(g,y)$ is a non-empty compact set. Note that ![]() $Q(g,y)$ is closed in
$Q(g,y)$ is closed in ![]() $X\times \lbrace\pm1\rbrace$. Hence
$X\times \lbrace\pm1\rbrace$. Hence ![]() $(Q(g_0,y)\cap Q(g,y))\subset Q(g_0,y)$ is compact. By Lemma 2.5, there exists a
$(Q(g_0,y)\cap Q(g,y))\subset Q(g_0,y)$ is compact. By Lemma 2.5, there exists a ![]() $\bar{g}\in C_0(Y)$ such that
$\bar{g}\in C_0(Y)$ such that
Pick ![]() $h\in C_0(X)$ such that
$h\in C_0(X)$ such that ![]() $T(h)=\bar{g}$. Find
$T(h)=\bar{g}$. Find ![]() $\{x,\lambda\}\in X\times \{\pm1\}$ such that
$\{x,\lambda\}\in X\times \{\pm1\}$ such that ![]() $\|h\|=\lambda h(x)$. For every
$\|h\|=\lambda h(x)$. For every ![]() $f\in T^{-1}(g)$,
$f\in T^{-1}(g)$,
 \begin{align*}
\|\bar{g}\|-\frac{1}{2}\varepsilon+\lambda f(x)&\leq\|h\|+\lambda f(x)=\lambda (h(x)+f(x))\\
&\leq\|h+f\|\leq\|T(h)+T(f)\|+\varepsilon\\
&=\|\bar{g}+g\|+\varepsilon=-\bar{g}(y)-g(y)+\varepsilon\\
&=\|\bar{g}\|-g(y)+\varepsilon.
\end{align*}
\begin{align*}
\|\bar{g}\|-\frac{1}{2}\varepsilon+\lambda f(x)&\leq\|h\|+\lambda f(x)=\lambda (h(x)+f(x))\\
&\leq\|h+f\|\leq\|T(h)+T(f)\|+\varepsilon\\
&=\|\bar{g}+g\|+\varepsilon=-\bar{g}(y)-g(y)+\varepsilon\\
&=\|\bar{g}\|-g(y)+\varepsilon.
\end{align*} This implies that  $-\lambda f(x)\geq g(y)-\frac{3}{2}\varepsilon$ and
$-\lambda f(x)\geq g(y)-\frac{3}{2}\varepsilon$ and ![]() $(x,-\lambda)\in Q(g,y)$. Similarly, we can show
$(x,-\lambda)\in Q(g,y)$. Similarly, we can show ![]() $(x,-\lambda)\in Q(g_0,y)$. Therefore,
$(x,-\lambda)\in Q(g_0,y)$. Therefore, ![]() $Q(g_0,y)\cap Q(g,y)$ is a non-empty compact set.
$Q(g_0,y)\cap Q(g,y)$ is a non-empty compact set.
Step III. We check that the set family ![]() $\lbrace Q(g,y)\cap Q(g_0,y)\rbrace_{g\in C_0(Y),\;g(y)\geq 0}$ has the finite intersection property. Fix
$\lbrace Q(g,y)\cap Q(g_0,y)\rbrace_{g\in C_0(Y),\;g(y)\geq 0}$ has the finite intersection property. Fix ![]() $g_1,g_2,...,g_n\in C_0(Y)$ with
$g_1,g_2,...,g_n\in C_0(Y)$ with ![]() $g_i(y)\geq 0$ for every
$g_i(y)\geq 0$ for every ![]() $i\in\{1,2,...,n\}$, by Lemma 2.5, there exists a
$i\in\{1,2,...,n\}$, by Lemma 2.5, there exists a ![]() $\bar{g}\in C_0(Y)$ such that
$\bar{g}\in C_0(Y)$ such that
Pick ![]() $h\in C_0(X)$ such that
$h\in C_0(X)$ such that ![]() $T(h)=\bar{g}$. Find
$T(h)=\bar{g}$. Find ![]() $\{x,\lambda\}\in X\times \{\pm1\}$ such that
$\{x,\lambda\}\in X\times \{\pm1\}$ such that ![]() $\|h\|=\lambda h(x)$. By the same argument as in Step II, we have
$\|h\|=\lambda h(x)$. By the same argument as in Step II, we have
Thus
Note that
Then ![]() $Q_+(y)$ is non-empty and the proof is complete.
$Q_+(y)$ is non-empty and the proof is complete.
Lemma 2.11. For every ![]() $x\in X$,
$x\in X$, ![]() $P_+(x)$ is a singleton.
$P_+(x)$ is a singleton.
Proof. Let ![]() $x\in X$, by Lemma 2.7,
$x\in X$, by Lemma 2.7, ![]() $P_+(x)$ is non-empty. Let
$P_+(x)$ is non-empty. Let ![]() $(y,\lambda)\in P_+(x)$, by Lemma 2.10,
$(y,\lambda)\in P_+(x)$, by Lemma 2.10, ![]() $Q_+(y)$ and
$Q_+(y)$ and ![]() $Q_-(y)$ are non-empty. For every
$Q_-(y)$ are non-empty. For every ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with ![]() $f(x) \gt 3\varepsilon$, we have
$f(x) \gt 3\varepsilon$, we have
 \begin{equation*}
\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon.
\end{equation*}
\begin{equation*}
\lambda T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon.
\end{equation*} If λ = 1, then  $T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon \gt 0$. For every
$T(f)(y)\geq f(x)-\frac{3}{2}\varepsilon \gt 0$. For every ![]() $(x',\mu)\in Q_+(y)$ and every
$(x',\mu)\in Q_+(y)$ and every ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with ![]() $f(x) \gt 3\varepsilon$, one has
$f(x) \gt 3\varepsilon$, one has
 \begin{equation}
\mu f(x')\geq T(f)(y)-\frac{3}{2}\varepsilon\geq f(x)-3\varepsilon \gt 0.
\end{equation}
\begin{equation}
\mu f(x')\geq T(f)(y)-\frac{3}{2}\varepsilon\geq f(x)-3\varepsilon \gt 0.
\end{equation} We assert that ![]() $x=x'$. Suppose on the contrary that
$x=x'$. Suppose on the contrary that ![]() $x\neq x'$, by the Urysohn lemma, there exists a
$x\neq x'$, by the Urysohn lemma, there exists a ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with ![]() $f(x) \gt 3\varepsilon$ and
$f(x) \gt 3\varepsilon$ and ![]() $f(x')=0$. This contradicts to (2.1). And hence we have
$f(x')=0$. This contradicts to (2.1). And hence we have ![]() $x=x'$ and µ = 1. Thus
$x=x'$ and µ = 1. Thus ![]() $Q_+(y)=\lbrace (x,\lambda)\rbrace$.
$Q_+(y)=\lbrace (x,\lambda)\rbrace$.
If ![]() $\lambda=-1$, then
$\lambda=-1$, then  $T(f)(y)\leq -(f(x)-\frac{3}{2}\varepsilon) \lt 0$. For every
$T(f)(y)\leq -(f(x)-\frac{3}{2}\varepsilon) \lt 0$. For every ![]() $(x',\mu)\in Q_-(y)$ and every
$(x',\mu)\in Q_-(y)$ and every ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with ![]() $f(x) \gt 3\varepsilon$, one has
$f(x) \gt 3\varepsilon$, one has
 \begin{equation*}
\mu f(x')\leq T(f)(y)+\frac{3}{2}\varepsilon\leq -(f(x)-\frac{3}{2}\varepsilon)+\frac{3}{2}\varepsilon=-f(x)+3\varepsilon \lt 0.\end{equation*}
\begin{equation*}
\mu f(x')\leq T(f)(y)+\frac{3}{2}\varepsilon\leq -(f(x)-\frac{3}{2}\varepsilon)+\frac{3}{2}\varepsilon=-f(x)+3\varepsilon \lt 0.\end{equation*} By the same argument as above, we have ![]() $x=x'$ and
$x=x'$ and ![]() $\mu=-1$. Thus
$\mu=-1$. Thus ![]() $Q_-(y)=\lbrace (x,\lambda)\rbrace$.
$Q_-(y)=\lbrace (x,\lambda)\rbrace$.
We assert that ![]() $P_+(x)$ is a singleton. Suppose on the contrary that there exist
$P_+(x)$ is a singleton. Suppose on the contrary that there exist ![]() $(y_1,\lambda_1)\neq(y_2,\lambda_2)\in P_+(x)$. By Remark 2.9,
$(y_1,\lambda_1)\neq(y_2,\lambda_2)\in P_+(x)$. By Remark 2.9, ![]() $y_1\neq y_2$. Without loss of generality, we assume that
$y_1\neq y_2$. Without loss of generality, we assume that ![]() $\lambda_1=1$. Then
$\lambda_1=1$. Then ![]() $Q_+(y_1)=\lbrace (x,1)\rbrace$. By the Urysohn lemma, there exists
$Q_+(y_1)=\lbrace (x,1)\rbrace$. By the Urysohn lemma, there exists ![]() $g\in C_0(Y)$ such that
$g\in C_0(Y)$ such that ![]() $g(y_1) \gt 3\varepsilon$ and
$g(y_1) \gt 3\varepsilon$ and ![]() $g(y_2)=0$. Then for every
$g(y_2)=0$. Then for every ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with ![]() $T(f)=g$, we have
$T(f)=g$, we have
 \begin{equation*}
f(x)\geq T(f)(y_1)-\frac{3}{2}\varepsilon=g(y_1)-\frac{3}{2}\varepsilon \gt 0.
\end{equation*}
\begin{equation*}
f(x)\geq T(f)(y_1)-\frac{3}{2}\varepsilon=g(y_1)-\frac{3}{2}\varepsilon \gt 0.
\end{equation*}Thus
 \begin{equation*}
0=\lambda_2g(y_2)=\lambda_2T(f)(y_2)\geq f(x)-\frac{3}{2}\varepsilon\geq g(y_1)-3\varepsilon \gt 0.
\end{equation*}
\begin{equation*}
0=\lambda_2g(y_2)=\lambda_2T(f)(y_2)\geq f(x)-\frac{3}{2}\varepsilon\geq g(y_1)-3\varepsilon \gt 0.
\end{equation*} This leads to a contradiction. Hence ![]() $P_+(x)$ is a singleton and the proof is complete.
$P_+(x)$ is a singleton and the proof is complete.
Similar to Lemma 2.11, we have the following result.
Lemma 2.12. For every ![]() $x\in X$,
$x\in X$, ![]() $P_-(x)$ is a singleton.
$P_-(x)$ is a singleton.
Lemma 2.13. For every ![]() $x\in X$,
$x\in X$, ![]() $P_+(x)=P_-(x)$.
$P_+(x)=P_-(x)$.
Proof. Fix ![]() $x\in X$, by Lemmas 2.11 and 2.12, there exist
$x\in X$, by Lemmas 2.11 and 2.12, there exist ![]() $y_1,\;y_2\in Y$ and
$y_1,\;y_2\in Y$ and ![]() $\lambda_1,\;\lambda_2\in \{\pm1\}$ such that
$\lambda_1,\;\lambda_2\in \{\pm1\}$ such that ![]() $P_+(x)=(y_1,\lambda_1)$ and
$P_+(x)=(y_1,\lambda_1)$ and ![]() $P_-(x)=(y_2,\lambda_2)$. According to the proofs of Lemma 2.11 and 2.12, we have
$P_-(x)=(y_2,\lambda_2)$. According to the proofs of Lemma 2.11 and 2.12, we have
 \begin{equation*}
(x,\lambda_1)=
\begin{cases}
&Q_+(y_1),\;\text{if}\;\lambda_1=1,\\
&Q_-(y_1),\;\text{if}\;\lambda_1=-1,
\end{cases}.
\;\;{\rm and}\;\;
(x,\lambda_2)=
\begin{cases}
&Q_-(y_2),\;\text{if}\;\lambda_2=1,\\
&Q_+(y_2),\;\text{if}\;\lambda_2=-1.
\end{cases}
\end{equation*}
\begin{equation*}
(x,\lambda_1)=
\begin{cases}
&Q_+(y_1),\;\text{if}\;\lambda_1=1,\\
&Q_-(y_1),\;\text{if}\;\lambda_1=-1,
\end{cases}.
\;\;{\rm and}\;\;
(x,\lambda_2)=
\begin{cases}
&Q_-(y_2),\;\text{if}\;\lambda_2=1,\\
&Q_+(y_2),\;\text{if}\;\lambda_2=-1.
\end{cases}
\end{equation*} We assert that ![]() $y_1=y_2$. Suppose on the contrary that
$y_1=y_2$. Suppose on the contrary that ![]() $y_1\neq y_2$, by the Urysohn lemma, there exists a
$y_1\neq y_2$, by the Urysohn lemma, there exists a ![]() $g\in C_0(Y)$ such that
$g\in C_0(Y)$ such that
For every ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with ![]() $T(f)=g$,
$T(f)=g$,
 \begin{equation*}\begin{cases}
f(x)\geq g(y_1)-\frac{3}{2}\varepsilon&\text{if $\lambda_1=1$},\\
-f(x)\leq g(y_1)+\frac{3}{2}\varepsilon
&\text{if $\lambda_1=-1$}.
\end{cases}\end{equation*}
\begin{equation*}\begin{cases}
f(x)\geq g(y_1)-\frac{3}{2}\varepsilon&\text{if $\lambda_1=1$},\\
-f(x)\leq g(y_1)+\frac{3}{2}\varepsilon
&\text{if $\lambda_1=-1$}.
\end{cases}\end{equation*}Thus
 \begin{equation}
f(x)\geq \lambda_1 g(y_1)-\frac{3}{2}\varepsilon.
\end{equation}
\begin{equation}
f(x)\geq \lambda_1 g(y_1)-\frac{3}{2}\varepsilon.
\end{equation} On the other hand, for every ![]() $f\in C_0(X)$ with
$f\in C_0(X)$ with ![]() $T(f)=g$,
$T(f)=g$,
 \begin{equation*}\begin{cases}
f(x)\leq -g(y_2)+\frac{3}{2}\varepsilon&\text{if $\lambda_2=1$},\\
-f(x)\geq -g(y_2)-\frac{3}{2}\varepsilon
&\text{if $\lambda_2=-1$}.
\end{cases}\end{equation*}
\begin{equation*}\begin{cases}
f(x)\leq -g(y_2)+\frac{3}{2}\varepsilon&\text{if $\lambda_2=1$},\\
-f(x)\geq -g(y_2)-\frac{3}{2}\varepsilon
&\text{if $\lambda_2=-1$}.
\end{cases}\end{equation*}Thus
 \begin{equation}
f(x)\leq-\lambda_2g(y_2)+\frac{3}{2}\varepsilon.
\end{equation}
\begin{equation}
f(x)\leq-\lambda_2g(y_2)+\frac{3}{2}\varepsilon.
\end{equation}Combining (2.2), (2.3) and (2.4), we have
 \begin{align*}
-\lambda_2g(y_2)+\frac{3}{2}\varepsilon&\geq f(x)\geq\lambda_1 g(y_1)-\frac{3}{2}\varepsilon \gt \lambda_2g(y_2)+\frac{3}{2}\varepsilon.
\end{align*}
\begin{align*}
-\lambda_2g(y_2)+\frac{3}{2}\varepsilon&\geq f(x)\geq\lambda_1 g(y_1)-\frac{3}{2}\varepsilon \gt \lambda_2g(y_2)+\frac{3}{2}\varepsilon.
\end{align*} This implies that ![]() $\lambda_2g(y_2) \lt 0$. By (2.2),
$\lambda_2g(y_2) \lt 0$. By (2.2), ![]() $\lambda_2g(y_2) \gt 0$. This leads to a contradiction and hence
$\lambda_2g(y_2) \gt 0$. This leads to a contradiction and hence ![]() $y_1=y_2$.
$y_1=y_2$.
Next we prove that ![]() $\lambda_1=\lambda_2$. Choose
$\lambda_1=\lambda_2$. Choose ![]() $f\in C_0(X)$ such that
$f\in C_0(X)$ such that ![]() $f(x) \gt 3\varepsilon$, then
$f(x) \gt 3\varepsilon$, then
 \begin{equation*}
\lambda_1T(f)(y_1)\geq f(x)-\frac{3}{2}\varepsilon \gt \frac{3}{2}\varepsilon,\; \lambda_2T(-f)(y_1)\leq-f(x)+\frac{3}{2}\varepsilon \lt -\frac{3}{2}\varepsilon.
\end{equation*}
\begin{equation*}
\lambda_1T(f)(y_1)\geq f(x)-\frac{3}{2}\varepsilon \gt \frac{3}{2}\varepsilon,\; \lambda_2T(-f)(y_1)\leq-f(x)+\frac{3}{2}\varepsilon \lt -\frac{3}{2}\varepsilon.
\end{equation*} If ![]() $\lambda_1\neq\lambda_2$, then
$\lambda_1\neq\lambda_2$, then
This leads to a contradiction. Hence ![]() $\lambda_1=\lambda_2$ and
$\lambda_1=\lambda_2$ and ![]() $P_+(x)=P_-(x)$. The proof is complete.
$P_+(x)=P_-(x)$. The proof is complete.
By a similar argument as Lemmas 2.11, 2.12 and 2.13, we can show the following result. To simplify this article, we omit its proof.
Lemma 2.14. For every ![]() $y\in Y$,
$y\in Y$, ![]() $Q_+(y)=Q_-(y)$ is a singleton.
$Q_+(y)=Q_-(y)$ is a singleton.
Remark 2.15. For every ![]() $x\in X$,
$x\in X$, ![]() $y\in Y$ and
$y\in Y$ and ![]() $\lambda\in\{\pm1\}$, by Lemmas 2.11, 2.12, 2.13 and 2.14, one has
$\lambda\in\{\pm1\}$, by Lemmas 2.11, 2.12, 2.13 and 2.14, one has
Now we are ready to show the main result of this paper.
Theorem 2.16. Let ![]() $T:C_0(X)\rightarrow C_0(Y)$ be a standard surjective ɛ-norm-additive map. Then there exists a homeomorphism
$T:C_0(X)\rightarrow C_0(Y)$ be a standard surjective ɛ-norm-additive map. Then there exists a homeomorphism ![]() $\varphi:Y\rightarrow X$ and a continuous function
$\varphi:Y\rightarrow X$ and a continuous function ![]() $\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that
$\lambda:Y\rightarrow\lbrace\pm1\rbrace$ such that
 \begin{equation*}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\;y\in Y,\;f\in C_0(X).
\end{equation*}
\begin{equation*}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\;y\in Y,\;f\in C_0(X).
\end{equation*}Proof. For ![]() $y\in Y$, by Lemma 2.14, there exist
$y\in Y$, by Lemma 2.14, there exist ![]() $x\in X$,
$x\in X$, ![]() $\lambda\in\{\pm1\}$ such that
$\lambda\in\{\pm1\}$ such that
Define
where ![]() $x, y, \lambda$ satisfy (2.5). Then
$x, y, \lambda$ satisfy (2.5). Then ![]() $\varphi:Y\rightarrow X$ and
$\varphi:Y\rightarrow X$ and ![]() $\lambda:Y\rightarrow\lbrace\pm1\rbrace$ are well defined. It follows from Remark 2.15 that φ is bijective. In what follows, we show that
$\lambda:Y\rightarrow\lbrace\pm1\rbrace$ are well defined. It follows from Remark 2.15 that φ is bijective. In what follows, we show that
 \begin{equation}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\;y\in Y,\;f\in C_0(X).
\end{equation}
\begin{equation}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\;y\in Y,\;f\in C_0(X).
\end{equation} Given ![]() $y\in Y$ and
$y\in Y$ and ![]() $f\in C_0(X)$. The proof is divided into two cases.
$f\in C_0(X)$. The proof is divided into two cases.
Case I. ![]() $f(\varphi(y))\geq0$. By Remark 2.15, we have
$f(\varphi(y))\geq0$. By Remark 2.15, we have ![]() $\{(y,\lambda(y)\}=P_+(\varphi(y))$. Then
$\{(y,\lambda(y)\}=P_+(\varphi(y))$. Then
 \begin{equation}
\lambda(y)T(f)(y)\geq f(\varphi(y))-\frac{3}{2}\varepsilon.
\end{equation}
\begin{equation}
\lambda(y)T(f)(y)\geq f(\varphi(y))-\frac{3}{2}\varepsilon.
\end{equation}We assert that
 \begin{equation}
\lambda(y)T(f)(y)\leq f(\varphi(y))+\frac{3}{2}\varepsilon.
\end{equation}
\begin{equation}
\lambda(y)T(f)(y)\leq f(\varphi(y))+\frac{3}{2}\varepsilon.
\end{equation} Suppose on the contrary that  $\lambda(y)T(f)(y) \gt f(\varphi(y))+\frac{3}{2}\varepsilon\geq0$. If
$\lambda(y)T(f)(y) \gt f(\varphi(y))+\frac{3}{2}\varepsilon\geq0$. If ![]() $\lambda(y)=1$, we have
$\lambda(y)=1$, we have ![]() $\{(\varphi(y),1\}=Q_+(y)$ and
$\{(\varphi(y),1\}=Q_+(y)$ and
 \begin{equation*}
f(\varphi(y))\geq T(f)(y)-\frac{3}{2}\varepsilon \gt f(\varphi(y)).
\end{equation*}
\begin{equation*}
f(\varphi(y))\geq T(f)(y)-\frac{3}{2}\varepsilon \gt f(\varphi(y)).
\end{equation*} This leads to a contradiction. If ![]() $\lambda(y)=-1$, we have
$\lambda(y)=-1$, we have ![]() $T(f)(y) \lt 0$ and
$T(f)(y) \lt 0$ and ![]() $\{(\varphi(y),-1\}=Q_+(y)=Q_-(y)$. Then
$\{(\varphi(y),-1\}=Q_+(y)=Q_-(y)$. Then
 \begin{equation*}
-f(\varphi(y))\leq T(f)(y)+\frac{3}{2}\varepsilon \lt -f(\varphi(y)).
\end{equation*}
\begin{equation*}
-f(\varphi(y))\leq T(f)(y)+\frac{3}{2}\varepsilon \lt -f(\varphi(y)).
\end{equation*}This is a contradiction. Combining (2.7) and (2.8), we have
 \begin{equation*}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon.
\end{equation*}
\begin{equation*}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon.
\end{equation*} Case II. ![]() $f(\varphi(y))\leq0$. By Remark 2.15 again, we have
$f(\varphi(y))\leq0$. By Remark 2.15 again, we have ![]() $\{(y,\lambda(y)\}=P_+(\varphi(y))=P_-(\varphi(y))$. Then
$\{(y,\lambda(y)\}=P_+(\varphi(y))=P_-(\varphi(y))$. Then
 \begin{equation}
\lambda(y)T(f)(y)\leq f(\varphi(y))+\frac{3}{2}\varepsilon.
\end{equation}
\begin{equation}
\lambda(y)T(f)(y)\leq f(\varphi(y))+\frac{3}{2}\varepsilon.
\end{equation}We assert that
 \begin{equation}
\lambda(y)T(f)(y)\geq f(\varphi(y))-\frac{3}{2}\varepsilon.
\end{equation}
\begin{equation}
\lambda(y)T(f)(y)\geq f(\varphi(y))-\frac{3}{2}\varepsilon.
\end{equation} Suppose on the contrary that  $\lambda(y)T(f)(y) \lt f(\varphi(y))-\frac{3}{2}\varepsilon\leq0$. If
$\lambda(y)T(f)(y) \lt f(\varphi(y))-\frac{3}{2}\varepsilon\leq0$. If ![]() $\lambda(y)=1$, we have
$\lambda(y)=1$, we have ![]() $\{(\varphi(y),1\}=Q_+(y)=Q_-(y)$ and
$\{(\varphi(y),1\}=Q_+(y)=Q_-(y)$ and
 \begin{equation*}
f(\varphi(y))\leq T(f)(y)+\frac{3}{2}\varepsilon \lt f(\varphi(y)).
\end{equation*}
\begin{equation*}
f(\varphi(y))\leq T(f)(y)+\frac{3}{2}\varepsilon \lt f(\varphi(y)).
\end{equation*} This leads to a contradiction. If ![]() $\lambda(y)=-1$, we have
$\lambda(y)=-1$, we have ![]() $Tf(y) \gt 0$ and
$Tf(y) \gt 0$ and ![]() $\{(\varphi(y),-1\}=Q_+(y)=Q_-(y)$. Then
$\{(\varphi(y),-1\}=Q_+(y)=Q_-(y)$. Then
 \begin{equation*}
-f(\varphi(y))\geq T(f)(y)-\frac{3}{2}\varepsilon \gt -f(\varphi(y)).
\end{equation*}
\begin{equation*}
-f(\varphi(y))\geq T(f)(y)-\frac{3}{2}\varepsilon \gt -f(\varphi(y)).
\end{equation*}This is a contradiction. Combining (2.9) and (2.10), we have
 \begin{equation*}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon.
\end{equation*}
\begin{equation*}
|T(f)(y)-\lambda(y)f(\varphi(y))|\leq\frac{3}{2}\varepsilon.
\end{equation*} Next we prove that φ is a homeomorphism and λ is continuous. Suppose that ![]() $\{y_\alpha\}_{\alpha\in\Lambda}\subset Y$ is a convergent net with
$\{y_\alpha\}_{\alpha\in\Lambda}\subset Y$ is a convergent net with ![]() $y_\alpha\rightarrow y$. Choose a compact neighbourhood U of y, without loss of generality, we can assume that
$y_\alpha\rightarrow y$. Choose a compact neighbourhood U of y, without loss of generality, we can assume that ![]() $\{y_\alpha\}_{\alpha\in\Lambda}\subset U$. By the Urysohn lemma, there exists a
$\{y_\alpha\}_{\alpha\in\Lambda}\subset U$. By the Urysohn lemma, there exists a ![]() $g\in C_0(Y)$ such that
$g\in C_0(Y)$ such that ![]() $g|_U\equiv 3\varepsilon+1$. By (2.6), for any
$g|_U\equiv 3\varepsilon+1$. By (2.6), for any ![]() $f\in C_0(X)$ with Tf = g, we obtain that
$f\in C_0(X)$ with Tf = g, we obtain that
 \begin{align*}
\frac{3}{2}\varepsilon&\geq|T(f)(y_\alpha)-\lambda(y_\alpha)f(\varphi(y_\alpha))|\\
&\geq|g(y_\alpha)|-|f(\varphi(y_\alpha))|\\
&=3\varepsilon+1-|f(\varphi(y_\alpha))|.
\end{align*}
\begin{align*}
\frac{3}{2}\varepsilon&\geq|T(f)(y_\alpha)-\lambda(y_\alpha)f(\varphi(y_\alpha))|\\
&\geq|g(y_\alpha)|-|f(\varphi(y_\alpha))|\\
&=3\varepsilon+1-|f(\varphi(y_\alpha))|.
\end{align*} This implies that  $|f(\varphi(y_\alpha))|\geq\frac{3}{2}\varepsilon+1$ and
$|f(\varphi(y_\alpha))|\geq\frac{3}{2}\varepsilon+1$ and ![]() $\{\varphi(y_\alpha)\}_{\alpha\in\Lambda}$ is contained in the compact set
$\{\varphi(y_\alpha)\}_{\alpha\in\Lambda}$ is contained in the compact set  $\lbrace x\in X: |f(x)|\geq\frac{3}{2}\varepsilon+1\rbrace$.
$\lbrace x\in X: |f(x)|\geq\frac{3}{2}\varepsilon+1\rbrace$.
By (2.6), for ![]() $\alpha\in\Lambda$, we have
$\alpha\in\Lambda$, we have
 \begin{equation}
|Tf(y_\alpha)-\lambda(y_\alpha)f(\varphi(y_\alpha))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\; f\in C_0(X).
\end{equation}
\begin{equation}
|Tf(y_\alpha)-\lambda(y_\alpha)f(\varphi(y_\alpha))|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\; f\in C_0(X).
\end{equation} For any convergent subnet ![]() $\{\varphi(y_{\alpha'})\}_{\alpha'\in \Lambda'}$ of
$\{\varphi(y_{\alpha'})\}_{\alpha'\in \Lambda'}$ of ![]() $\{\varphi(y_\alpha)\}_{\alpha\in\Lambda}$ with
$\{\varphi(y_\alpha)\}_{\alpha\in\Lambda}$ with ![]() $\varphi(y_{\alpha'})\rightarrow x$, let
$\varphi(y_{\alpha'})\rightarrow x$, let ![]() $\{\lambda(y_{\alpha''})\}_{\alpha''\in \Lambda''}$ be a convergent subnet of
$\{\lambda(y_{\alpha''})\}_{\alpha''\in \Lambda''}$ be a convergent subnet of ![]() $\{\lambda(y_{\alpha'})\}_{\alpha'\in\Lambda'}$ with
$\{\lambda(y_{\alpha'})\}_{\alpha'\in\Lambda'}$ with ![]() $\lambda(y_{\alpha''})\rightarrow \lambda$. By (2.11), we have
$\lambda(y_{\alpha''})\rightarrow \lambda$. By (2.11), we have
 \begin{equation*}
|T(f)(y)-\lambda f(x)|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\; f\in C_0(X).
\end{equation*}
\begin{equation*}
|T(f)(y)-\lambda f(x)|\leq\frac{3}{2}\varepsilon,\;{\rm for\;all}\; f\in C_0(X).
\end{equation*} This implies that ![]() $\{(x,\lambda)\}=Q_+(y)$ and hence
$\{(x,\lambda)\}=Q_+(y)$ and hence ![]() $\varphi(y)=x$. Thus φ is continuous. By the same argument, we can get φ −1 is also continuous. Hence φ is a homeomorphism. For any convergent subset
$\varphi(y)=x$. Thus φ is continuous. By the same argument, we can get φ −1 is also continuous. Hence φ is a homeomorphism. For any convergent subset ![]() $\{\lambda(y_{\alpha'})\}_{\alpha'\in \Lambda'}$ of
$\{\lambda(y_{\alpha'})\}_{\alpha'\in \Lambda'}$ of ![]() $\{\lambda(y_\alpha)\}_{\alpha\in\Lambda}$ with
$\{\lambda(y_\alpha)\}_{\alpha\in\Lambda}$ with ![]() $\lambda(y_{\alpha'})\rightarrow \lambda$, by (2.11) again, we have
$\lambda(y_{\alpha'})\rightarrow \lambda$, by (2.11) again, we have
 \begin{equation*}
|T(f)(y)-\lambda f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\; {\rm for\;all}\;f\in C_0(X).
\end{equation*}
\begin{equation*}
|T(f)(y)-\lambda f(\varphi(y))|\leq\frac{3}{2}\varepsilon,\; {\rm for\;all}\;f\in C_0(X).
\end{equation*} This implies that ![]() $\{(\varphi(y),\lambda)\}=Q_+(y)$ and
$\{(\varphi(y),\lambda)\}=Q_+(y)$ and ![]() $\lambda(y)=\lambda$. Hence
$\lambda(y)=\lambda$. Hence ![]() $\lambda: Y\rightarrow \{\pm1\}$ is continuous. The proof is complete.
$\lambda: Y\rightarrow \{\pm1\}$ is continuous. The proof is complete.
The following example shows that the estimate ‘![]() $\frac{3}{2}\varepsilon$’ in Theorem 2.16 is optimal.
$\frac{3}{2}\varepsilon$’ in Theorem 2.16 is optimal.
Example 2.17. Let ![]() $X=\{x_1, x_2\}$ with the discrete topology, then
$X=\{x_1, x_2\}$ with the discrete topology, then ![]() $C(X)=\ell_\infty^2$. Let
$C(X)=\ell_\infty^2$. Let
 \begin{equation*}
U_1=\{(a,b)\in C(X):b\leq-\frac{1}{2}\varepsilon,\;a+b\geq-\frac{1}{2}\varepsilon,\;(a,b)\neq(\varepsilon,-\frac{1}{2}\varepsilon)\}
\end{equation*}
\begin{equation*}
U_1=\{(a,b)\in C(X):b\leq-\frac{1}{2}\varepsilon,\;a+b\geq-\frac{1}{2}\varepsilon,\;(a,b)\neq(\varepsilon,-\frac{1}{2}\varepsilon)\}
\end{equation*}and
 \begin{equation*}
U_2=C(X)\setminus(U_1\cup\{(0,0),(\varepsilon,-\frac{1}{2}\varepsilon)\}).
\end{equation*}
\begin{equation*}
U_2=C(X)\setminus(U_1\cup\{(0,0),(\varepsilon,-\frac{1}{2}\varepsilon)\}).
\end{equation*} Define ![]() $T:C(X)\to C(X)$ by
$T:C(X)\to C(X)$ by
 \begin{equation*}
T((a,b))= \left\{
\begin{array}{ll}
(0,0) & (a,b)=(0,0),\\
(\varepsilon,\varepsilon) & (a,b)=(\varepsilon,-\frac{1}{2}\varepsilon),\\
(a-\frac{1}{2}\varepsilon,b) & (a,b)\in U_1,\\
(a,b-\frac{1}{2}\varepsilon) &(a,b)\in U_2.\\
\end{array}\right.
\end{equation*}
\begin{equation*}
T((a,b))= \left\{
\begin{array}{ll}
(0,0) & (a,b)=(0,0),\\
(\varepsilon,\varepsilon) & (a,b)=(\varepsilon,-\frac{1}{2}\varepsilon),\\
(a-\frac{1}{2}\varepsilon,b) & (a,b)\in U_1,\\
(a,b-\frac{1}{2}\varepsilon) &(a,b)\in U_2.\\
\end{array}\right.
\end{equation*}It is not difficult to verify that T is a standard surjective map. In what follows, we show that T is an ɛ-norm-additive map. By the definition of T,
 \begin{align*}
\|T(f)-f\|\leq\frac{1}{2}\varepsilon,\;\forall\;f\in C(X),\; f\neq(\varepsilon,-\frac{1}{2}\varepsilon).
\end{align*}
\begin{align*}
\|T(f)-f\|\leq\frac{1}{2}\varepsilon,\;\forall\;f\in C(X),\; f\neq(\varepsilon,-\frac{1}{2}\varepsilon).
\end{align*} Then for any ![]() $f,g\in C(X)$ with
$f,g\in C(X)$ with  $f,g\neq(\varepsilon,-\frac{1}{2}\varepsilon)$, we have
$f,g\neq(\varepsilon,-\frac{1}{2}\varepsilon)$, we have
 \begin{align*}
\big|\|T(f)+T(g)\|-\|f+g\|\big|&\leq\|(T(f)+T(g))-(f+g)\|\\
&\leq\|T(f)-f\|+\|T(g)-g\|\leq\varepsilon.
\end{align*}
\begin{align*}
\big|\|T(f)+T(g)\|-\|f+g\|\big|&\leq\|(T(f)+T(g))-(f+g)\|\\
&\leq\|T(f)-f\|+\|T(g)-g\|\leq\varepsilon.
\end{align*} The left case is  $f=(\varepsilon,-\frac{1}{2}\varepsilon)$ and
$f=(\varepsilon,-\frac{1}{2}\varepsilon)$ and ![]() $g\in C(X)$. When
$g\in C(X)$. When ![]() $g=(0,0)$ or
$g=(0,0)$ or  $(\varepsilon,-\frac{1}{2}\varepsilon)$, it is clear that
$(\varepsilon,-\frac{1}{2}\varepsilon)$, it is clear that
Let ![]() $g=(a,b)\in U_1$, we have
$g=(a,b)\in U_1$, we have
 \begin{align*}
|b+\varepsilon|\leq|b|\leq a+\frac{1}{2}\varepsilon.
\end{align*}
\begin{align*}
|b+\varepsilon|\leq|b|\leq a+\frac{1}{2}\varepsilon.
\end{align*}Then
 \begin{align*}
\|T(f)+T(g)\|=&\max\{|a+\frac{1}{2}\varepsilon|,|b+\varepsilon|\}=a+\frac{1}{2}\varepsilon,\\
\|f+g\|=&\max\{|a+\varepsilon|,|b-\frac{1}{2}\varepsilon|\}=a+\varepsilon.
\end{align*}
\begin{align*}
\|T(f)+T(g)\|=&\max\{|a+\frac{1}{2}\varepsilon|,|b+\varepsilon|\}=a+\frac{1}{2}\varepsilon,\\
\|f+g\|=&\max\{|a+\varepsilon|,|b-\frac{1}{2}\varepsilon|\}=a+\varepsilon.
\end{align*}Thus
 \begin{align*}
\big|\|T(f)+T(g)\|-\|f+g\|\big|=\frac{1}{2}\varepsilon.
\end{align*}
\begin{align*}
\big|\|T(f)+T(g)\|-\|f+g\|\big|=\frac{1}{2}\varepsilon.
\end{align*} Let ![]() $g=(a,b)\in U_2$, we have
$g=(a,b)\in U_2$, we have
 \begin{align*}
\big|\|T(f)+T(g)\|-\|f+g\|\big|&=\big|\|(a+\varepsilon, b+\frac{1}{2}\varepsilon)\|-\|(a+\varepsilon, b-\frac{1}{2}\varepsilon)\|\big|\\
&\leq\|(a+\varepsilon, b+\frac{1}{2}\varepsilon)-(a+\varepsilon, b-\frac{1}{2}\varepsilon)\|\\
&=\|(0,\varepsilon)\|=\varepsilon.
\end{align*}
\begin{align*}
\big|\|T(f)+T(g)\|-\|f+g\|\big|&=\big|\|(a+\varepsilon, b+\frac{1}{2}\varepsilon)\|-\|(a+\varepsilon, b-\frac{1}{2}\varepsilon)\|\big|\\
&\leq\|(a+\varepsilon, b+\frac{1}{2}\varepsilon)-(a+\varepsilon, b-\frac{1}{2}\varepsilon)\|\\
&=\|(0,\varepsilon)\|=\varepsilon.
\end{align*} Therefore, T is an ɛ-norm-additive map. The homeomorphism ![]() $\varphi:X\rightarrow X$ and
$\varphi:X\rightarrow X$ and ![]() $\lambda:X\rightarrow\{\pm1\}$ which satisfy Theorem 2.16 are
$\lambda:X\rightarrow\{\pm1\}$ which satisfy Theorem 2.16 are
When  $f=(\varepsilon,-\frac{1}{2}\varepsilon)$, then
$f=(\varepsilon,-\frac{1}{2}\varepsilon)$, then
 \begin{equation*}
|T(f)(x_2)-\lambda(x_2)f(\varphi(x_2))|=|\varepsilon-(-\frac{1}{2}\varepsilon)|=\frac{3}{2}\varepsilon.
\end{equation*}
\begin{equation*}
|T(f)(x_2)-\lambda(x_2)f(\varphi(x_2))|=|\varepsilon-(-\frac{1}{2}\varepsilon)|=\frac{3}{2}\varepsilon.
\end{equation*} This implies that the estimate ![]() $\frac{3}{2}\varepsilon$ in Theorem 2.16 is optimal.
$\frac{3}{2}\varepsilon$ in Theorem 2.16 is optimal.
Remark 2.18. The assumption of surjectivity of T in Theorem 2.16 is essential in general. For instance, let ![]() $X=\{a\}$,
$X=\{a\}$, ![]() $Y=\{b,c\}$ be two discrete topological spaces, then
$Y=\{b,c\}$ be two discrete topological spaces, then ![]() $C(X)=\mathbb{R}$ and
$C(X)=\mathbb{R}$ and ![]() $C(Y)=\ell_\infty^2$. Define
$C(Y)=\ell_\infty^2$. Define ![]() $T:\mathbb{R}\rightarrow \ell_\infty^2$ by
$T:\mathbb{R}\rightarrow \ell_\infty^2$ by ![]() $T(x)=(x,\sin x)$ for all
$T(x)=(x,\sin x)$ for all ![]() $x\in\mathbb{R}$. Then T is a norm-additive map, but X and Y are not homeomorphic.
$x\in\mathbb{R}$. Then T is a norm-additive map, but X and Y are not homeomorphic.
Acknowledgements
The authors are grateful to the referee and the editor for their constructive comments and helpful suggestions.
Funding Statement
Longfa Sun is supported by the National Natural Science Foundation of China (Grant no. 12101234), the Natural Science Foundation of Hebei Province (Grant no. A2022502010), the Fundamental Research Funds for the Central Universities (Grant no. 2023MS164) and the China Scholarship Council.