Hostname: page-component-7bb8b95d7b-2h6rp Total loading time: 0 Render date: 2024-09-06T05:32:03.283Z Has data issue: false hasContentIssue false
  • English
  • Français

Orbifold Zeta Functions for Dual Invertible Polynomials

Part of: Theory of singularities and catastrophe theory Affine geometry Surfaces and higher-dimensional varieties Differential topology

Published online by Cambridge University Press:  23 May 2016

Wolfgang Ebeling  and
Sabir M. Gusein-Zade
Wolfgang Ebeling
Affiliation:
Leibniz Universität Hannover, Institut für Algebraische Geometrie, Postfach 6009, 30060 Hannover, Germany ([email protected])
Sabir M. Gusein-Zade
Affiliation:
Moscow State University, Faculty of Mechanics and Mathematics, Moscow, GSP-1, 119991, Russia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

An invertible polynomial in n variables is a quasi-homogeneous polynomial consisting of n monomials so that the weights of the variables and the quasi-degree are well defined. In the framework of the construction of mirror symmetric orbifold Landau–Ginzburg models, Berglund, Hübsch and Henningson considered a pair (f, G) consisting of an invertible polynomial f and an abelian group G of its symmetries together with a dual pair 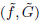. Here we study the reduced orbifold zeta functions of dual pairs (f, G) and 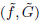and show that they either coincide or are inverse to each other depending on the number n of variables.

Keywords

invertible polynomialgroup actionmonodromyorbifold zeta function

MSC classification

Secondary: 14J33: Mirror symmetry 14R20: Group actions on affine varieties 57R18: Topology and geometry of orbifolds 58K10: Monodromy
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 1 , February 2017 , pp. 99 - 106
Copyright
Copyright © Edinburgh Mathematical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)