Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T21:06:09.782Z Has data issue: false hasContentIssue false
  • English
  • Français

On topological approaches to the Jacobian conjecture in ℂn

Part of: Theory of singularities and catastrophe theory Differential topology Affine geometry Partial differential equations General first-order equations and systems Families, fibrations

Published online by Cambridge University Press:  07 May 2020

Francisco Braun ,
Luis Renato Gonçalves Dias  and
Jean Venato-Santos
Francisco Braun
Affiliation:
Departamento de Matemática, Universidade Federal de São Carlos, 13565-905 São Carlos, São Paulo, Brazil ([email protected])
Luis Renato Gonçalves Dias
Affiliation:
Faculdade de Matemática, Universidade Federal de Uberlândia, 38408-100 Uberlândia, Minas Gerais, Brazil ([email protected] and [email protected])
Jean Venato-Santos
Affiliation:
Faculdade de Matemática, Universidade Federal de Uberlândia, 38408-100 Uberlândia, Minas Gerais, Brazil ([email protected] and [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain a new theorem for the non-properness set 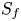$S_f$ of a non-singular polynomial mapping 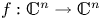$f:\mathbb C^n \to \mathbb C^n$. In particular, our result shows that if f is a counterexample to the Jacobian conjecture, then 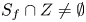$S_f\cap Z \neq \emptyset $, for every hypersurface Z dominated by 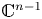$\mathbb C^{n-1}$ on which some non-singular polynomial 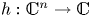$h: \mathbb C^{n}\to \mathbb C$ is constant. Also, we present topological approaches to the Jacobian conjecture in 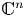$\mathbb C^n$. As applications, we extend bidimensional results of Rabier, Lê and Weber to higher dimensions.

Keywords

Jacobian conjectureglobal injectivitylocally trivial fibrationsnon-properness set

MSC classification

Primary: 14R15: Jacobian problem 14D06: Fibrations, degenerations 58K15: Topological properties of mappings 57R45: Singularities of differentiable mappings
Secondary: 35F05: Linear first-order equations 35A30: Geometric theory, characteristics, transformations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 3 , August 2020 , pp. 666 - 675
Check for updates
Copyright
Copyright © The Authors, 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Abhyankar, S. and Moh, T. T., Embeddings of the line in the plane, J. Reine Angew. Math. 276 (1975), 148–166.Google Scholar
2.Adjamagbo, K. and van den Essen, A., A resultant criterion and formula for the inversion of a polynomial map in two variables, J. Pure Appl. Alg. 64 (1990), 1–6.CrossRefGoogle Scholar
3.Bass, H., Connell, E. and Wright, D., The Jacobian conjecture: reduction of degree and formal expansion of the inverse, Bull. Amer. Math. Soc. 7 (1982), 287–330.CrossRefGoogle Scholar
4.Campbell, L. A., The asymptotic variety of a Pinchuk map as a polynomial curve, Appl. Math. Lett. 24 (2011), 62–65.CrossRefGoogle Scholar
5.Cynk, S. and Rusek, K., Injective endomorphisms of algebraic and analytic sets, Ann. Polonici Math. 56 (1991), 29–35.CrossRefGoogle Scholar
6.Dias, L. R. G., Ruas, M. A. S. and Tibăr, M., Regularity at infinity of real mappings and a Morse–Sard theorem, J. Topology 5 (2012), 323–340.CrossRefGoogle Scholar
7.van den Essen, A., A criterion to decide if a polynomial map is invertible and to compute the inverse, Commun. in Algebra 18(10) 1990), 3183–3186.Google Scholar
8.van den Essen, A., Polynomial automorphisms and the Jacobian conjecture, Progress in Mathematics, Volume 190 (Birkhäuser, 2000).CrossRefGoogle Scholar
9.Gurjar, R. V., Topology of affine varieties dominated by an affine space, Invent. Math. 59 (1980), 221–225.CrossRefGoogle Scholar
10.Hà, H. V., Nombres de Lojasiewicz et singularités à l'infini des polynômes de deux variables complexes, C. R. Acad. Sci. Paris Sér. I Math. 311 (1990), 429–432.Google Scholar
11.Hubbers, E., The Jacobian conjecture: cubic homogeneous maps in dimension four, Master's thesis, University of Nijmegen, 1994.Google Scholar
12.Jelonek, Z., The set of points at which a polynomial map is not proper, Ann. Polon. Math. 58 (1993), 259–266.CrossRefGoogle Scholar
13.Jelonek, Z., Testing sets for properness of polynomial mappings, Math. Ann. 315 (1999), 1–35.CrossRefGoogle Scholar
14.Jelonek, Z., Geometry of real polynomial mappings, Math. Z. 239 (2002), 321–333.CrossRefGoogle Scholar
15.Jelonek, Z., On the generalized critical values of a polynomial mapping, Manuscripta Math. 110 (2003), 145–157.CrossRefGoogle Scholar
16.Jelonek, Z. and Kurdyka, K., Reaching generalized critical values of a polynomial, Math. Z. 276 (2014), 557–570.CrossRefGoogle Scholar
17Joiţa, C. and Tibăr, M., Bifurcation set of multi-parameter families of complex curves, J. Topol. 11 (2018), 739–751.CrossRefGoogle Scholar
18.Krasiński, T. and Spodzieja, S., On linear differential operators related to the n-dimensional Jacobian conjecture, Lecture Notes in Mathematics, Volume 1524, pp. 308–315 (Springer-Verlag, 1992).CrossRefGoogle Scholar
19.Kurdyka, K., Orro, P. and Simon, S., Semialgebraic Sard theorem for generalized critical values, J. Differ. Geom. 56 (2000), 67–92.CrossRefGoogle Scholar
20.Lê, D. T. and Weber, C., A geometrical approach to the Jacobian conjecture for n = 2, Koday Math. J. 17 (1994), 374–381.Google Scholar
21.Maquera, C. and Venato-Santos, J., Foliations and global injectivity in $\mathbb {R}^n$, Bull. Braz. Math. Soc. 44 (2013), 273–284.CrossRefGoogle Scholar
22.Parusiński, A., On the bifurcation set of a complex polynomial with isolated singularities at infinity, Compositio Math. 97 (1995), 369–384.Google Scholar
23.Păunescu, L. and Zaharia, A., On the Łojasiewicz exponent at infinity for polynomial functions, Kodai Math. J. 20 (1997), 269–274.CrossRefGoogle Scholar
24.Pinchuck, S., A counterexample to the strong real Jacobian conjecture, Math. Z. 217 (1994), 1–4.CrossRefGoogle Scholar
25.Rabier, P. J., Ehresmann fibrations and Palais–Smale conditions for morphisms of Finsler manifolds, Ann. Math. 146 (1997), 647–691.CrossRefGoogle Scholar
26.Rusek, K. and Winiarski, T., Criteria for regularity of holomorphic mappings, Bull. Acad. Polon. Sci. Sér. Sci. Math. 28 (1980), 471–475.Google Scholar
27.Siersma, D. and Tibăr, M., Singularities at infinity and their vanishing cycles, Duke Math. J. 80 (1995), 771–783.CrossRefGoogle Scholar
28.Steenrod, N., The topology of fibre bundles (Princeton University Press, 1951).CrossRefGoogle Scholar
29.Verdier, J. L., Stratifications de Whitney et théorème de Bertini–Sard, Invent. Math. 36 (1976), 295–312.CrossRefGoogle Scholar